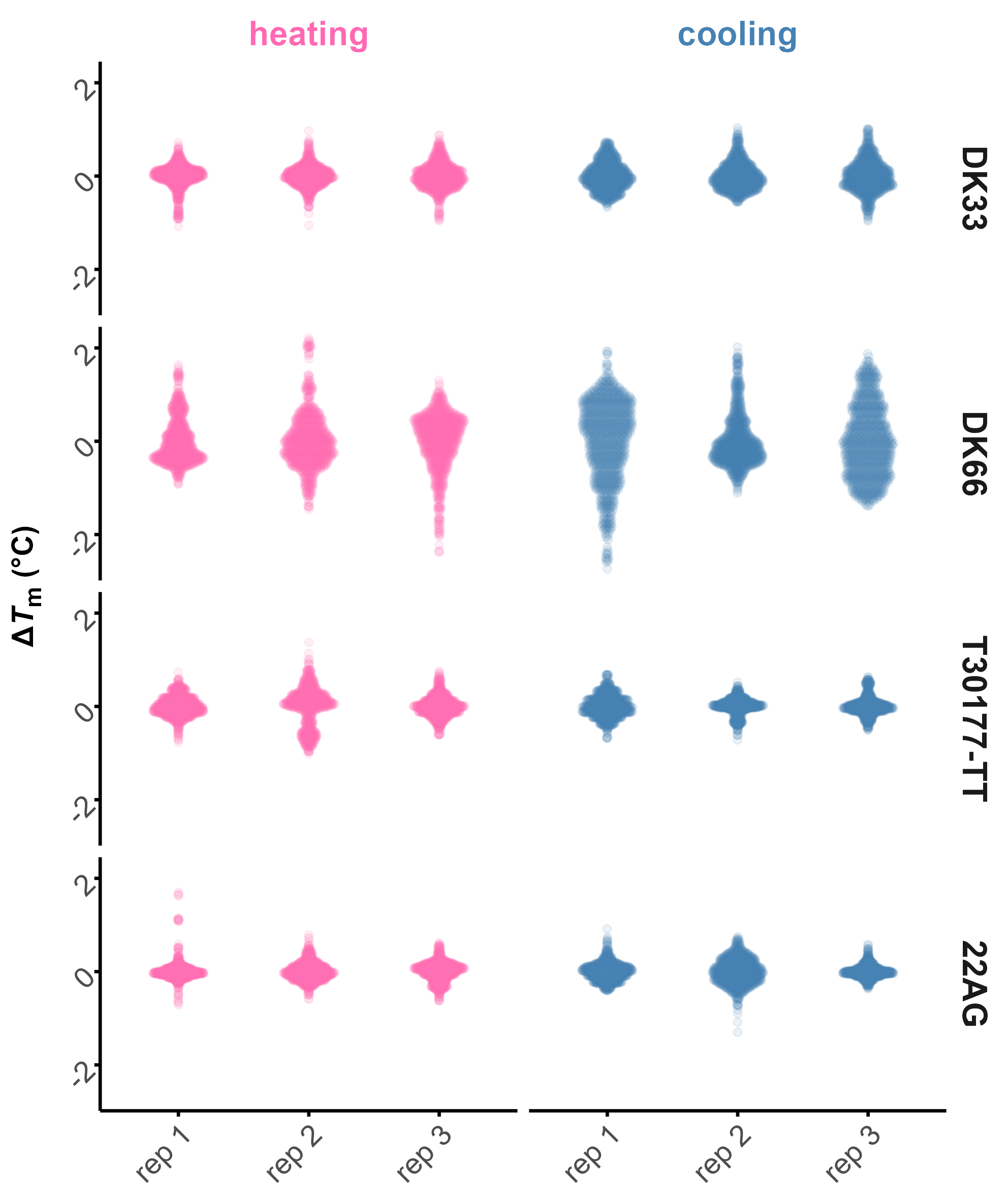5  Thèmes de recherche à l’Université de Bordeaux : résultats et perspectives

5.1 Contexte

Je suis recruté par l’Université de Bordeaux en tant que maître de conférences en 2017 (Figure 5.1). Le poste est attribué au laboratoire de chimie analytique de l’UFR de pharmacie (Bordeaux, campus Carreire) pour les aspects pédagogiques, et à l’équipe BALI (Biophysics Analysis and Ligands) de Valérie Gabelica au sein du laboratoire ARNA (INSERM U1212, CNRS UMR 5315, Université de Bordeaux), à l’Institut Européen de Chimie et Biologie (IECB, Pessac), pour la recherche.

J’étais le seul autre chercheur permanent de l’équipe jusqu’au départ de Valérie Gabelica fin 2023 (Figure 5.2), si l’on omet la présence de Frédéric Rosu, l’indispensable ingénieur de recherche de la plateforme de spectrométrie de masse. Peu de ce qui suit aurait été possible sans lui. L’équipe était spécialiste de la spectrométrie de masse native pour étudier des complexes non-covalents, en particulier ceux formés par les acides nucléiques. Je n’introduirai pas ici cette thématique, le lecteur pouvant se référer à une récente revue exhaustive de l’équipe [1]. Fin 2023, je rejoint l’équipe PRISM de Cameron Mackereth et déménage au bâtiment Bordeaux Biologie Santé (BBS, Bordeaux, campus Carreire), toujours chez ARNA.

Durant ces premières années comme maître de conférences, j’ai dirigé la thèse de Matthieu Ranz grâce à une ADT qui m’a été accordée en 2021 par l’Université de Bordeaux (soutenue en 2024). J’ai également coencadré la thèse d’Alexander König, dirigée par Valérie (soutenue en 2023).

Mes thèmes de recherche actuels sont centrés sur le développement et l’utilisation de méthodes analytiques et computationnelles pour caractériser les structures secondaires, dynamiques et interactions d’acides nucléiques, et en particulier les G4s. Bien que ces structures soient maintenant connues depuis plusieurs décennies, leur important polymorphisme les rend difficiles à étudier par des méthodes de référence (RMN, cristallographie). Ci-après, je décris brièvement les différents axes que je développe pour mieux comprendre comment ces structures, et d’autres, se forment, se comportent et interagissent. Dans ce qui suit, les Sections 5.2 à 5.5 ont été initiées dans l’équipe BALI, et les suivantes chez PRISM.

Figure 5.1. L’équipe BALI en septembre 2017. De gauche à droite : Stefano Piccolo, Eric Largy, Frédéric Rosu, Valérie Gabelica, Sandrine Livet, Nina Khristenko, Clémence Rabin, Anirban Ghosh et Steven Daly

Figure 5.2. L’équipe BALI en 2022, sans la cheffe ! : Eric Largy, Corinne Buré, Matthieu Ranz, Alexander Konig, Frédéric Rosu et Dominika Strzelecka. Crédit photo : Inserm/François Guénet.

5.2 HDX/MS de bio-macromolécules

5.2.1 HDX/MS native d’acides nucléiques

5.2.1.1 Preuve de concept

Alors que l’échange hydrogène-deutérium couplé à la spectrométrie de masse (HDX/MS) est relativement répandu pour étudier la dynamique de protéines (voir Section 4.4), il n’était cependant pas exploité pour étudier les acides nucléiques. Lors de ma prise de poste à l’Université de Bordeaux, je me suis attaché à montrer qu’il s’y prête, offrant des perspectives pour explorer les structure et dynamique d’acides nucléiques, et leurs interactions avec des protéines (Figure 5.3) [2].

Figure 5.3. A. L’HDX repose sur l’échange d’hydrogène et de deutérium en fonction du “statut” de la liaison hydrogène et son accessibilité au solvant. B. Les G-quadruplexes ont été utilisés comme modèles parce que les G-quartets qu’ils contiennent sont formés par un réseau de huit liaisons hydrogène avec les fonctions imino (orange) et amino (bleu) qui peuvent être échangées sur une large plage de temps. C. Pour mesurer les cinétiques d’échange rapide (1-300 s), un montage de mélange en flux continu a été utilisé, en utilisant une vanne à 6 ports et 2 positions pour changer facilement de taille de capillaire (nuances de gris ; les lignes en pointillés illustrent le couplage direct d’un capillaire à la source MS pour raccourcir le temps de mélange). Figure reproduite avec permission [2].

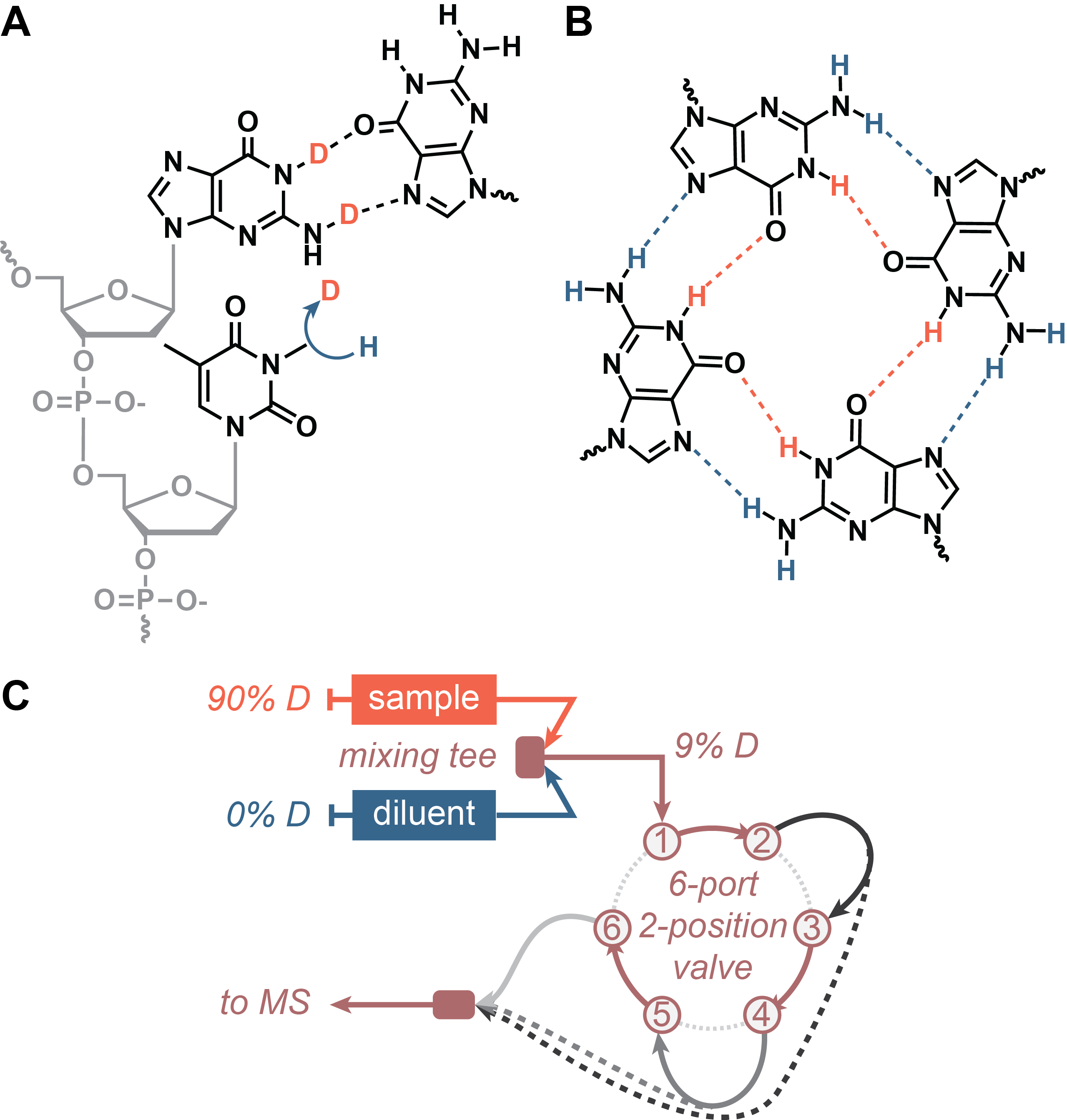
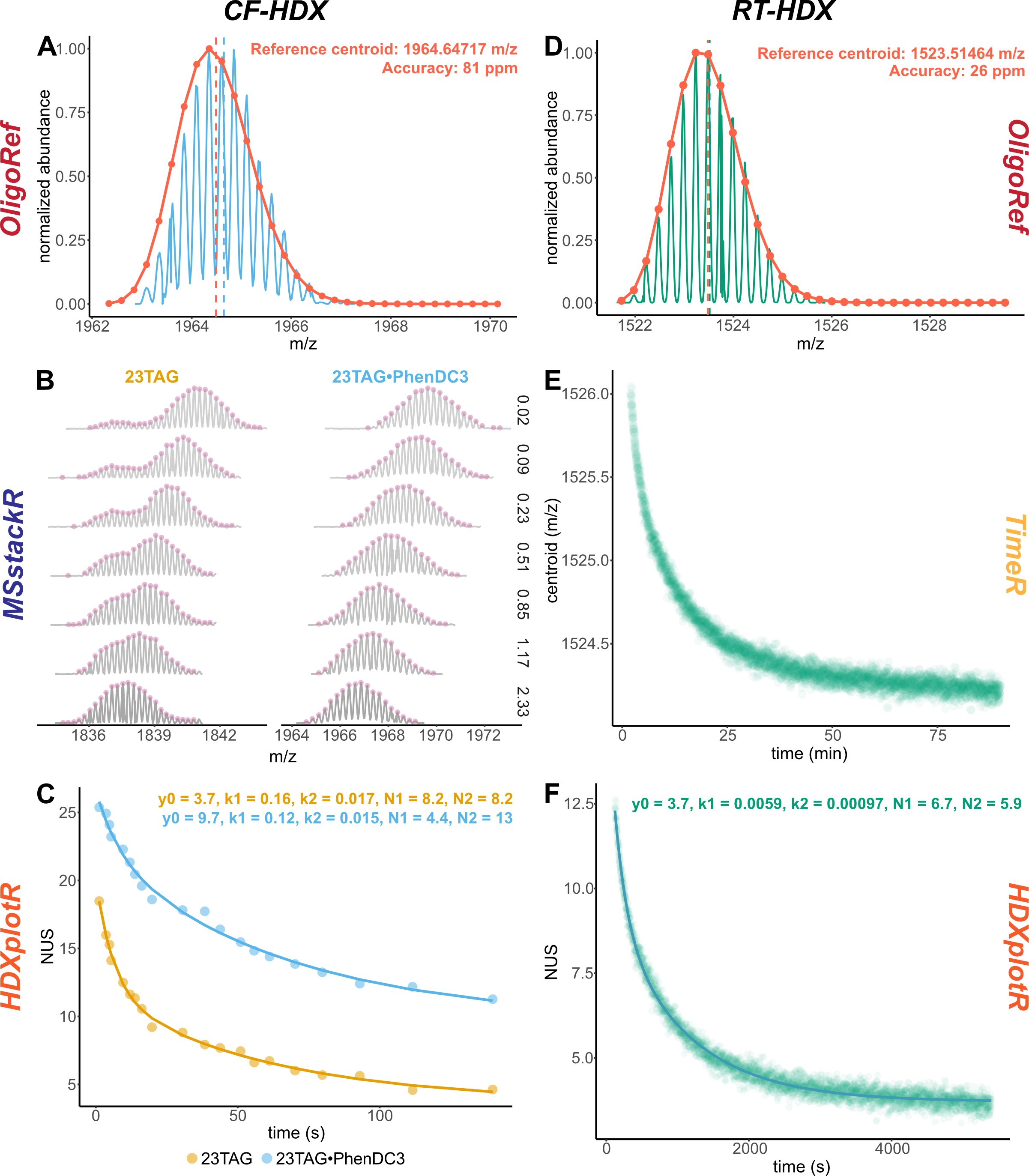
J’ai ainsi mis en place des méthodes de mesure d’échange allant de la seconde à plusieurs jours, couplées à la spectrométrie de masse native, et donc applicables à l’étude de complexes non-covalents d’acides nucléiques (Figure 5.3A). Deux techniques ont été développées :

1. Mesure en temps réel de l’échange (RT-HDX) : le mélange d’une solution d’ADN pré-déutéré avec un tampon non-déutéré déclenche l’échange. Cette solution est ensuite infusée dans le spectromètre de masse, chaque scan correspondant à un temps précis de déutération.

2. Mélange en flux continu (CF-HDX) : les analytes pré-déutérés sont mélangés avec un tampon non-déutéré avant d’être introduits dans le spectromètre de masse. Le temps d’échange est contrôlé par le débit et le volume entre le point de mélange et le spectromètre (Figure 5.3C). Tous les scans MS correspondant au même temps de déutération.

Ces méthodes, très différentes des approches bottom-up appliquées aux protéines, nous ont permis de démontrer que :

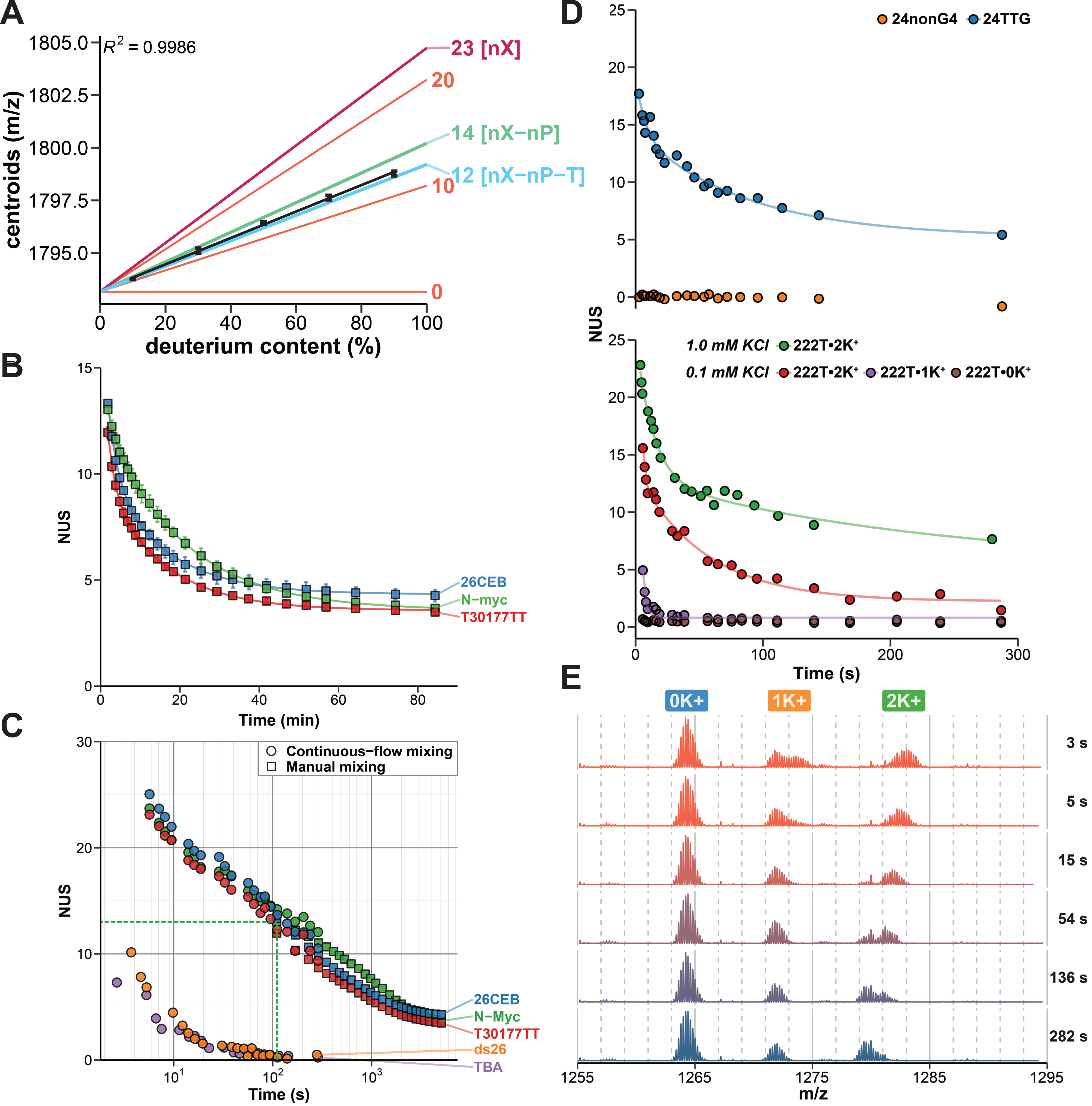
1. Les nucléobases échangent proportionnellement au ratio H/D en solution (Figure 5.4A), ce qui permet de modéliser les distributions isotopiques ; un point critique pour modéliser les données (voir Section 5.4.3).

2. Les vitesses d’échange peuvent être mesurées de façon précise et exacte, ce qui est idéal pour des applications en contrôle qualité par exemple (Figure 5.4B), et sur une large gamme de temps, adaptée à différentes structures (Figure 5.4C).

3. Les vitesses d’échange sont fortement dépendantes de l’appariement de ces bases et leurs interactions intermoléculaires avec de petites molécules, elles reflètent donc les structures des analytes (Figure 5.4D).

4. Le couplage à la spectrométrie de masse native permet de mesurer les cinétiques d’échange individuelles de complexes non covalents, pour ceux qui sont séparés en masse (Figure 5.4E). Cela permet l’utilisation de la méthode pour des études biophysiques d’acides nucléiques (Section 5.2.1.2).

Figure 5.4. A. Proportionnalité entre la deutération des nucléotides et le pourcentage de deutérium en solution par mesure de ESI-MS native (nX : nombre de sites sur les bases, nP : nombre de phosphates neutralisés, T : nombre de sites des termini 5’ et 3’). B. Mesures d’HDX/MS de trois G4s en triplicat (barres d’erreur : 1 écart-type). C. Mesure d’HDX/MS sur une large gamme de temps d’échange, en utilisant les mélanges en flux continu et manuel. D. Seuls les oligonucléotides structurés (bleu, vert, rouge, violet ; G4s) sont protégés de l’échange et le degré de protection dépend de la structure. Les oligonucléotides non structurés (orange, marron) échangent dans le temps mort. E. Les cinétiques d’échanges de plusieurs complexes non covalents peuvent être mesurées simultanément grâce à la séparation en masse native. Ici l’oligonucléotide 222T est en équilibre entre les formes non structurées (0 K⁺), G4 à deux tétrades (1 K⁺), et G4 à trois tétrades (2 K⁺), dont les cinétiques sont visibles dans le panneau D. L’échange a lieu dans la direction D \(\rightarrow\) H, donc les distributions isotopiques se déplacent vers les bas \(m/z\), et donc de droite à gauche. Figure adaptée avec permission [2].

Pour ces premiers travaux, j’ai encadré plusieurs étudiants : Anaïs Ferrer (DEUST, Bordeaux), Yann Bourdeau, (Licence, Bordeaux ; maintenant en thèse dirigée par I. Bestel, Bordeaux), Laura Fricot (Master, Bordeaux) et Émile Feugas (Pharmacien, Master, Bordeaux).

Ce projet, financé depuis octobre 2021 par une ANR JCJC, vise désormais à établir l’HDX/MS comme une méthode de choix pour l’analyse de structures et dynamique d’acides nucléiques, en travaillant autour de trois axes :

1. Etablir les bases fondamentales de l’HDX/MS d’acides nucléiques, pour interpréter les vitesses d’échanges en termes d’équilibre et de dynamique, en mesurant les vitesses d’échange intrinsèques des nucléotides par RMN ;

2. Développer une approche HDX/MS native top-down, qui couplera une séparation par MS native (par masse et forme) et une fragmentation MS/MS pour obtenir des données à l’échelle du nucléotide pour des analytes séparés par masse et structure ;

3. Appliquer ces développements méthodologiques pour répondre à des questions de biophysique des acides nucléiques (thermodynamique et cinétiques de structuration), caractériser les modes interactions entre acides nucléiques et des petites molécules ou protéines d’intérêt thérapeutique, et pour améliorer le contrôle qualité d’oligonucléotides thérapeutiques (structures d’aptamères, tests de stress, comparaison de lots, etc.)

C’est dans ce cadre de ce projet financé par l’ANR que j’ai fait une demande d’ADT, qui m’a été accordée pour la direction de la thèse de Matthieu Ranz. Je présente brièvement ci-dessous nos avancées sur ce projet.

5.2.1.2 Application à la biophysique des G4s

Nous avons appliqué nos méthodes HDX/masse native à un large panel d’oligonucléotides se structurant en G4 de conformations et stabilités diverses [3]. Cela nous a permis de confirmer les résultats de nos premier travaux et d’établir plusieurs points importants :

1. Une large gamme de temps de deutération est nécessaire pour observer l’échange de tous les sites structurés des G4s.

2. Le couplage à la masse native permet de mesurer simultanément les cinétiques d’échange de plusieurs espèces dans un mélange conformationnel.

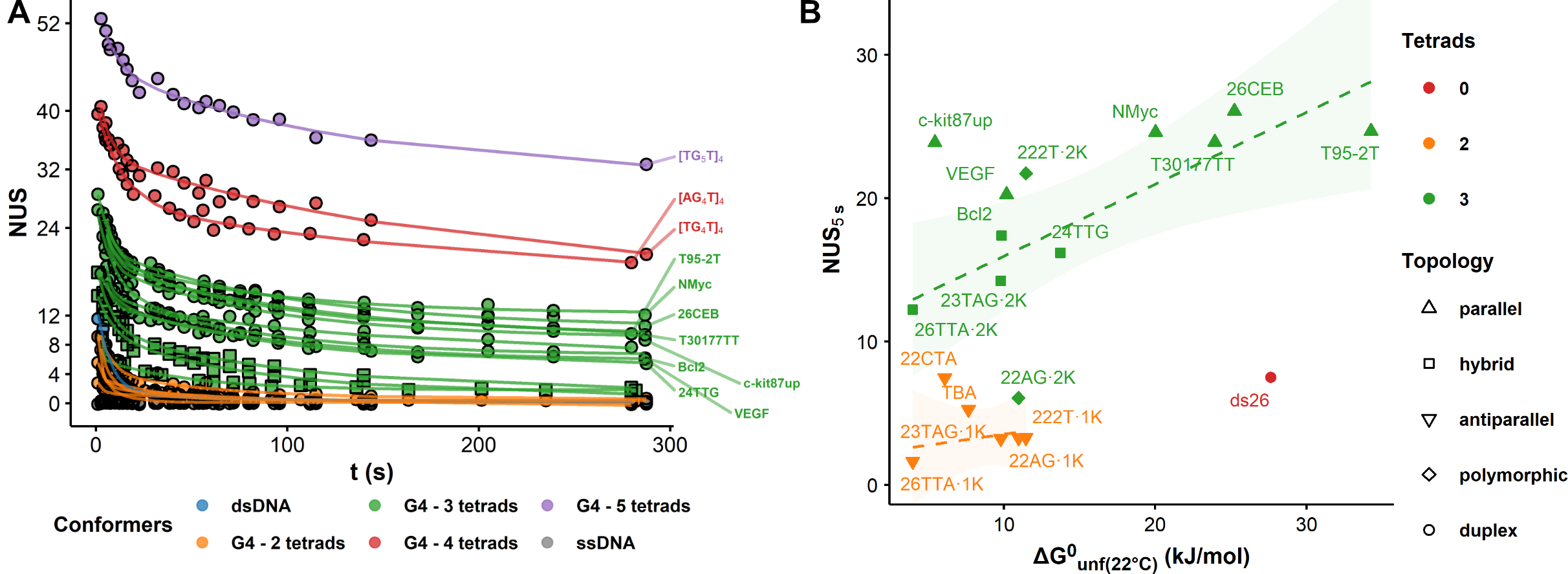
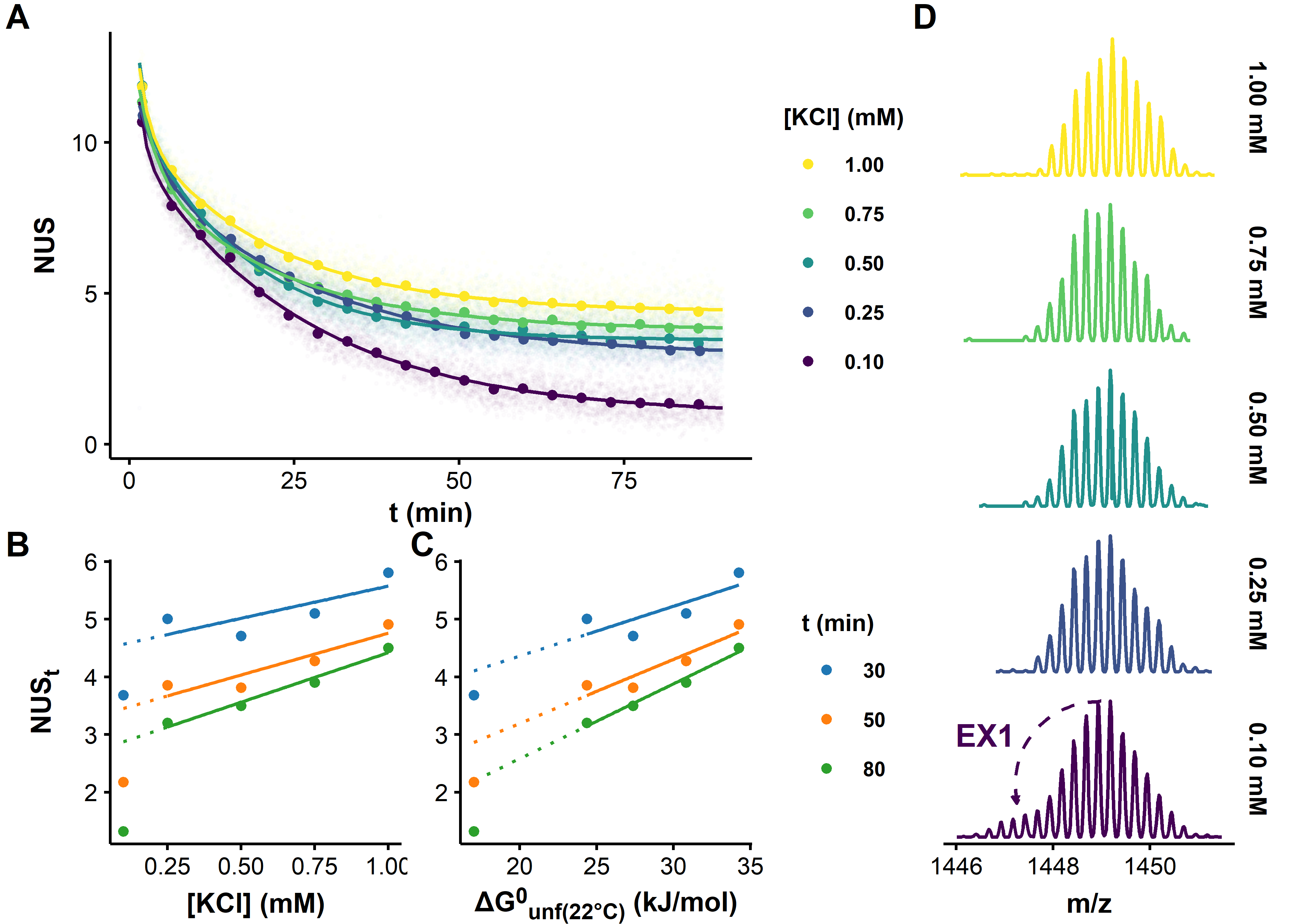
3. Le nombre de sites protégés reflète, entre autres, le nombre de tétrades d’un G4. Nous avons mis à disposition un set de données de référence pour déterminer le nombre de tétrades à partir d’une cinétique HDX (Figure 5.5A) [4].

4. La vitesse d’échange diminue lorsque la stabilité (\(T_m\), \(\Delta G^0\)) d’un G4 augmente, mais elle dépend également de la dynamique conformationnel et de l’éventuel présence de motifs non canoniques (Figures 5.5B et 5.7A-C). Contrairement aux stabilités évaluées par melting, l’HDX/MS a l’avantage d’être une mesure isotherme, sans déplacement de l’équilibre conformationnel dû aux changements de température.

4. Largy, E., Ranz, M. et Gabelica, V. DNA-HDXMS_XchangeDB: A dataset of Hydrogen-Deuterium eXchange native Mass Spectrometry experiments on DNA oligonucleotides. 2023, 10.5281/ZENODO.7713144.

Figure 5.5. Les cinétiques d’échange HDX dépendent de la structure, du nombre de tétrades, et de la stabilité du G4. A. Cinétiques d’échange (NUS = nombre de sites non échangés) d’oligonucléotides G4, duplex et déstructurés (ssDNA). B. Relation entre le nombre de sites non échangés après 5 secondes et l’énergie libre de déstructuration. Figure reproduite avec permission [3].

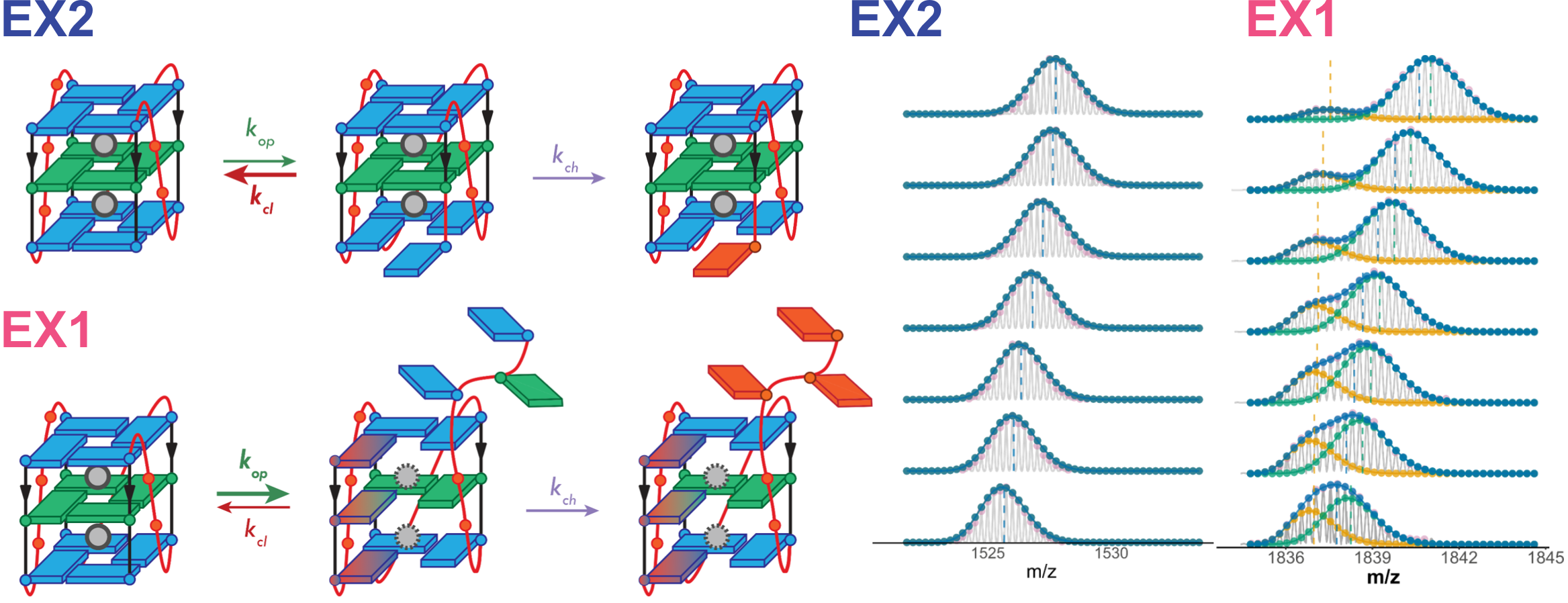
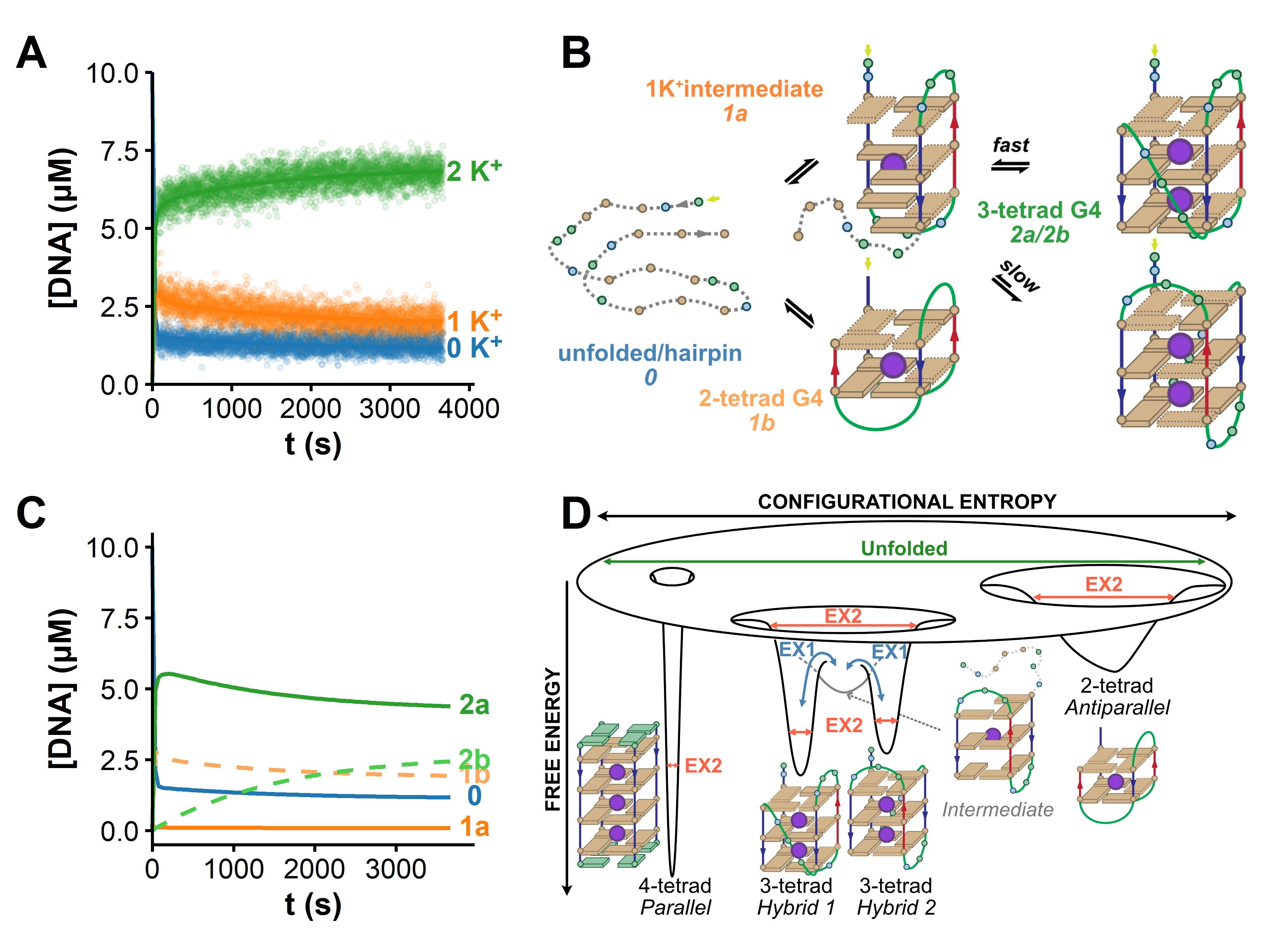
Le mécanisme de l’échange dépend donc de la stabilité, du nombre de tétrades et de la topologie des G4s. Nous avons identifiés deux cas limites (Figure 5.6) :

1. Les G4s stables échangent rarement, et un site à la fois, via des fluctuations locales (‘EX2’). Pour les duplexes, on parlerait de respiration, comme définit par von Hippel il y a plus de soixante ans [5, 6]. Cela se traduit par un déplacement, lent, de la distribution isotopique sur l’axe des m/z.

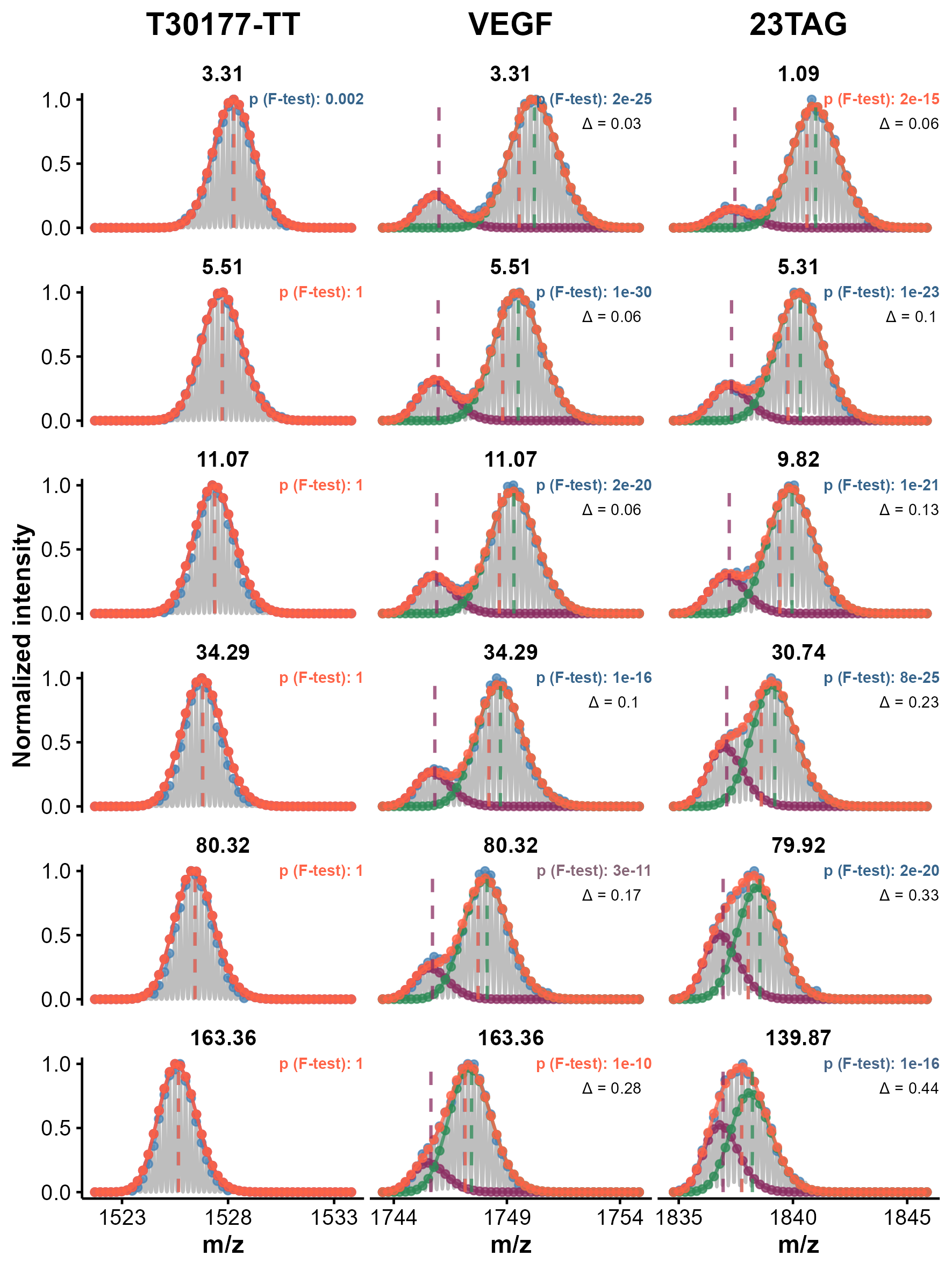
2. Les G4s peu stables, particulièrement ceux à deux tétrades (mais pas uniquement), peuvent aussi échanger plusieurs sites coopérativement via déstructuration partielle ou totale (‘EX1’, Figures 5.7 et 5.8B). Cela se traduit par la formation d’une seconde distribution isotopique, plus échangée que la première, et donc d’une distribution bimodale. L’intensité de la distribution originale diminue, et celle de la seconde augmente d’autant au cours de la réaction. Il est probable que la topologie du G4 influence la nature des états partiellement déstructurés. Surtout, ces états peuvent être détectés par HDX même si cette population est invisible par d’autres techniques car très peu peuplée et très transitoire. Ces cinétiques EX1 peuvent être exploitées, par déconvolution des distributions isotopiques bimodales qu’elles produisent, afin de déterminer les vitesses de déstructuration et le nombre de sites protégés des états déstructurés, ce qui permet de mieux caractériser les paysages énergétiques des G4s (Figure 5.8).

5. Hippel, P.H. von, Johnson, N.P. et Marcus, A.H. Fifty years of DNA “Breathing”: Reflections on old and new approaches. Biopolymers, 2013, 99, 923.

6. Kabir, A., Bhattarai, M., Rasmussen, K.Ø., Shehu, A., Usheva, A., Bishop, A.R. et Alexandrov, B. Examining DNA breathing with pyDNA-EPBD. Bioinformatics, 2023, 39.

Figure 5.6. Schéma de principe des régimes d’échange limites EX2 et EX1 (gauche) et distributions isotopiques caractéristiques correspondantes, pendant l’échange (de haut en bas pour un échange D vers H).

Figure 5.7. A. Cinétique HDX/native MS de l’aptamère anti-HIV1 T95-2T, formant un G4 parallèle en présence de différentes concentrations de KCl. B et C. Le nombre de sites protégés après 30, 50 ou 80 minutes d’échange augmente avec la concentration en KCl et avec la stabilité du G4 (qui augmente elle-même avec la concentration en KCl). Cette relation est linéaire pour un échange EX2. Lorsque l’échange se fait partiellement par EX1, la relation n’est plus linéaire. Ici, le G4 a été déstabilisé en réduisant la concentration de KCl à 0.10 mM. D. Spectres de masse de T95-2T après 6 minutes d’échange montrant la présence d’une distribution isotopique bimodale à 0.10 mM en KCl, caractéristique du mécanisme EX1. La population ayant échangé plusieurs sites coopérativement apparaît à gauche de la distribution majoritaire car elle est significativement moins deutérée (échange D \(\rightarrow\) H). Figure reproduite avec permission [3].

Figure 5.8. Structuration et déstructuration du G4 télomérique humain 23TAG. A. Cinétique de coordination du K⁺ (1 mM) et de 23TAG (10 μM) dans 100 mM de TMAA (pH 7.0). Les lignes sont le résultat de la modélisation dynamique utilisant le mécanisme de structuration du panneau B. C. Simulation de la concentration des ensembles individuels à partir des constantes de vitesse optimisées. D. Relation entre le paysage énergétique des G4s et le mécanisme d’échange. L’augmentation du nombre de tétrades donne des entonnoirs plus profonds et plus étroits. Plus l’entonnoir est étroit, plus l’échange EX2 est lent. L’échange EX1 nécessite que l’oligonucléotide visite d’autres états qui peuvent être des intermédiaires de structuration (par exemple, G-triplex) entre différentes topologies. Figure reproduite avec permission [3].

On notera qu’une même espèce peut échanger par EX2 et EX1, ce qui produit des distributions bimodales avec changements concertés d’intensité (EX1) et déplacement de ces deux distributions sur l’axe des m/z (EX2). Enfin, la présence d’autres conformères de même masse mais de cinétiques d’échanges distinctes ajoute des distributions supplémentaires. Un exemple de distribution trimodale est donnée dans la Figure 5.11. Nous avons mis en place des outils logiciels pour traiter ce type de données complexes (Section 5.4.3), mais cela peut être insuffisant. Nous avons donc ajouté une dimension de séparation supplémentaire, décrite ci-dessous.

5.2.1.3 Couplage à la mobilité ionique

Les travaux ci-avant se heurtent à une limite : l’incapacité de séparer les conformères de même masse… par masse. Nous développons donc actuellement le couplage de l’HDX à la spectrométrie de mobilité ionique (IMS). Il s’agit d’une partie importante des travaux de thèse de de Matthieu Ranz. Romane Guisiano a également participé à ce projet comme stagiaire de M2, et est désormais en thèse sous la direction de Ralf Jockers (Université Paris Cité, Institut Cochin, UM 3, UMR 8104, UMR-S 1016).

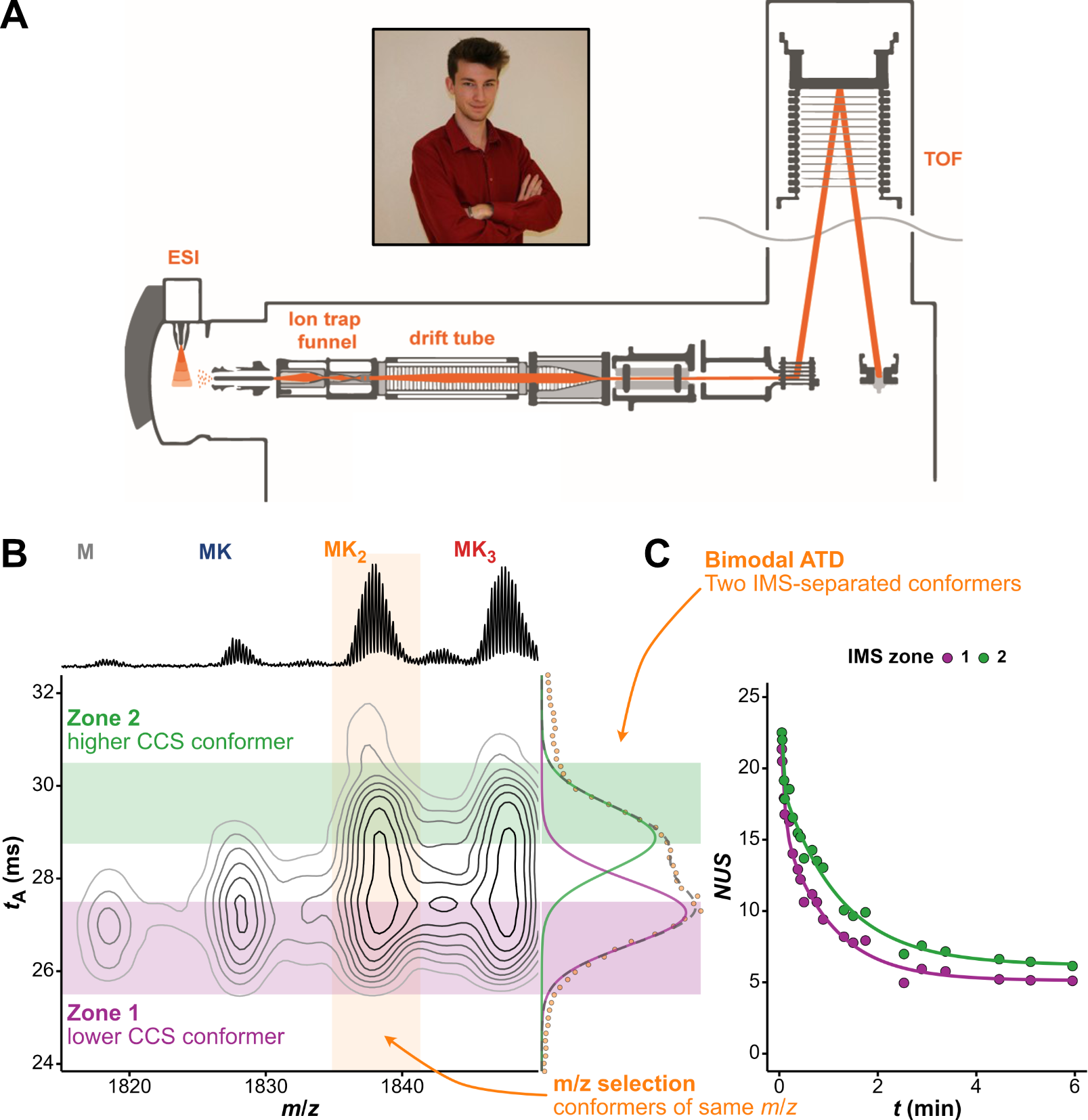
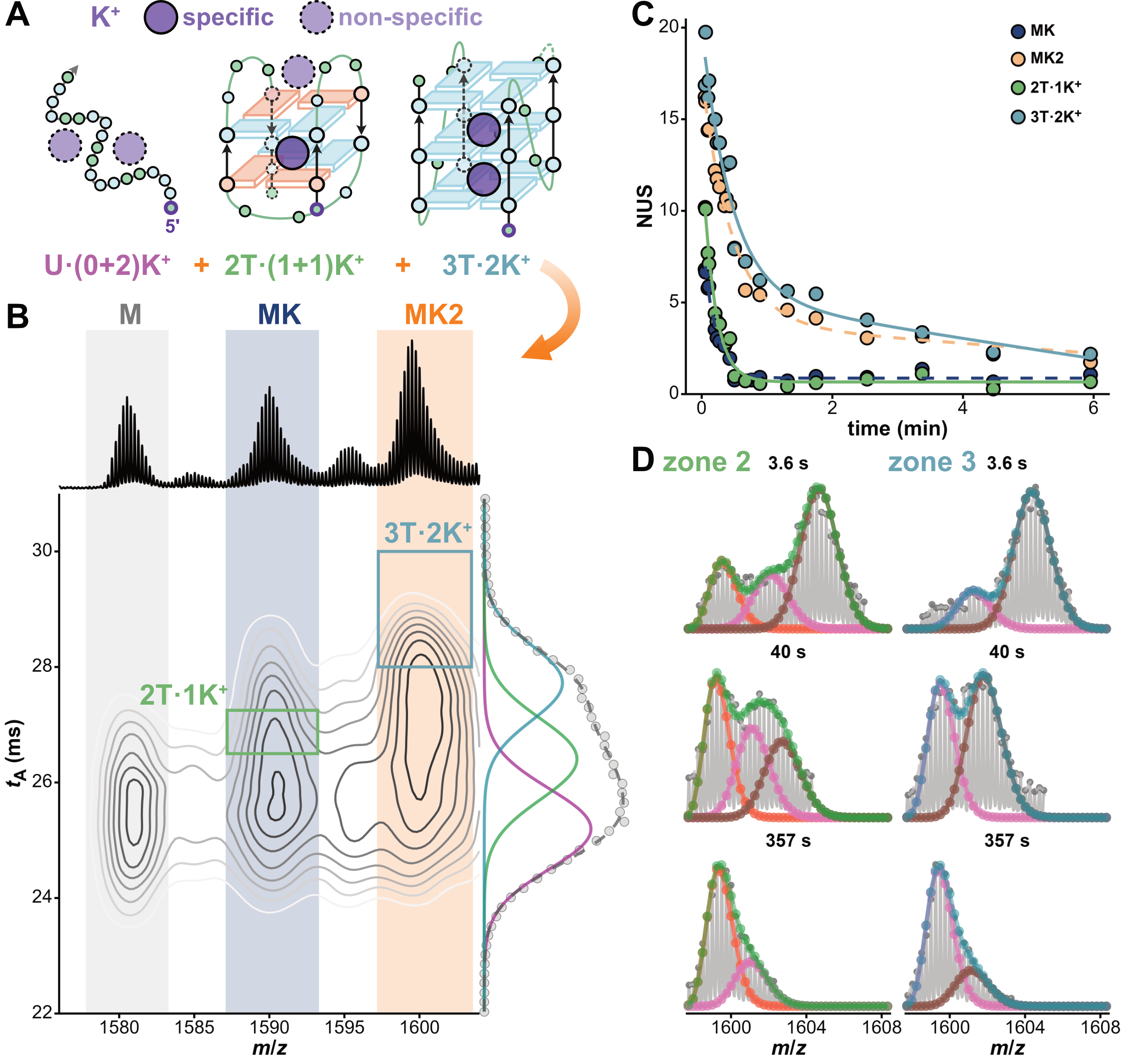
Il existe plusieurs façon de réaliser une séparation IMS. Ici, on utilise un spectromètre de masse équipé d’un tube de dérive (Figure 5.9A). Brièvement, les ions d’oligonucléotides générés dans la source du spectromètre de masse sont introduits par paquet dans le tube de dérive contenant un gaz (généralement de l’azote, mais ici de l’hélium). Lorsque les ions se déplacent dans le tube, par application d’un champ électrique, ils entrent en collision avec le gaz, ce qui ralentit leur mouvement en fonction de leur section efficace de collision (schématiquement, les plus gros ions sont davantage ralentis). Différents conformères peuvent donc être séparés en fonction de leur mobilité ionique, avant d’atteindre le détecteur du spectromètre de masse [7]. Cela vient s’ajouter à la séparation en masse, où l’on prend toujours soin de conserver les interactions non-covalentes intacts. Ainsi, dans la Figure 5.9B, les conformères sont séparés par masse sur l’axe des abscisses et par IMS sur l’axe des ordonnées. Les cinétiques d’échange de la Figure 5.9C ont été déterminées par sélection en masse de l’espèce liant 2 K⁺ (MK₂, orange), pour laquelle on a séparé deux conformères par IMS (vert et violet).

7. Gabelica, V. et Marklund, E. Fundamentals of ion mobility spectrometry. Current Opinion in Chemical Biology, 2018, 42, 51.

Figure 5.9. Principe de l’HDX/IMS-MS native. A. Schéma d’un spectromètre de masse Agilent ESI-Q-TOF équipé d’un tube de dérive pour la séparation IMS. Encart : Matthieu Ranz. B. Contour plot construit à partir des données HDX/IMS-MS native de 23TAG en présence d’1 mM de KCl. C. Cinétiques d’échange isotopique apparentes pour deux conformères séparés en IMS, formés par 23TAG·2K⁺.

Le couplage à l’HDX a nécessité d’optimiser les paramètres expérimentaux, notamment au niveau de la source et du fragmenteur du spectromètre de masse, pour obtenir un compromis satisfaisant entre rapport signal/bruit et résolution de ces conformères par leur temps d’arrivée (t_A).

Les résultats de l’étude d’un panel de G4s par HDX/IMS-MS native peuvent être classés en trois catégories décrites ci-dessous.

5.2.1.3.1 Cas 1 : Plusieurs conformères en solution, de même masse, avec des CCS et cinétiques d’échange distinctes

Dans ce cas de figure, les conformères ne sont pas séparables par masse, mais le sont par IMS, ce qui permet d’accéder à leur cinétique d’échange propre. Nos résultats actuels montrent que nous sommes capables de résoudre des systèmes complexes, comme par exemple celui de la séquence télomérique humaine 23TAG (Figure 5.9B,C), pour laquelle nous avons discriminé les topologies hybrides 1 et 2 visibles dans la Figure 5.8B. Nous avons observé un échange plus rapide de la topologie hybride 2, qui ne s’explique pas par une différence de stabilité entre ces topologies, mais par une dynamique de déstructuration plus rapide. En effet, la déconvolution de leurs distributions isotopiques pendant l’échange, désormais résolues en IMS, permet de montrer que l’hybride 2 se déstructure plus vite que l’hybride 1 (0.57 min^-1 vs. 1.76 min^-1, respectivement, en EX1), alors que leur échange par fluctuation locale (EX2) est similaire.

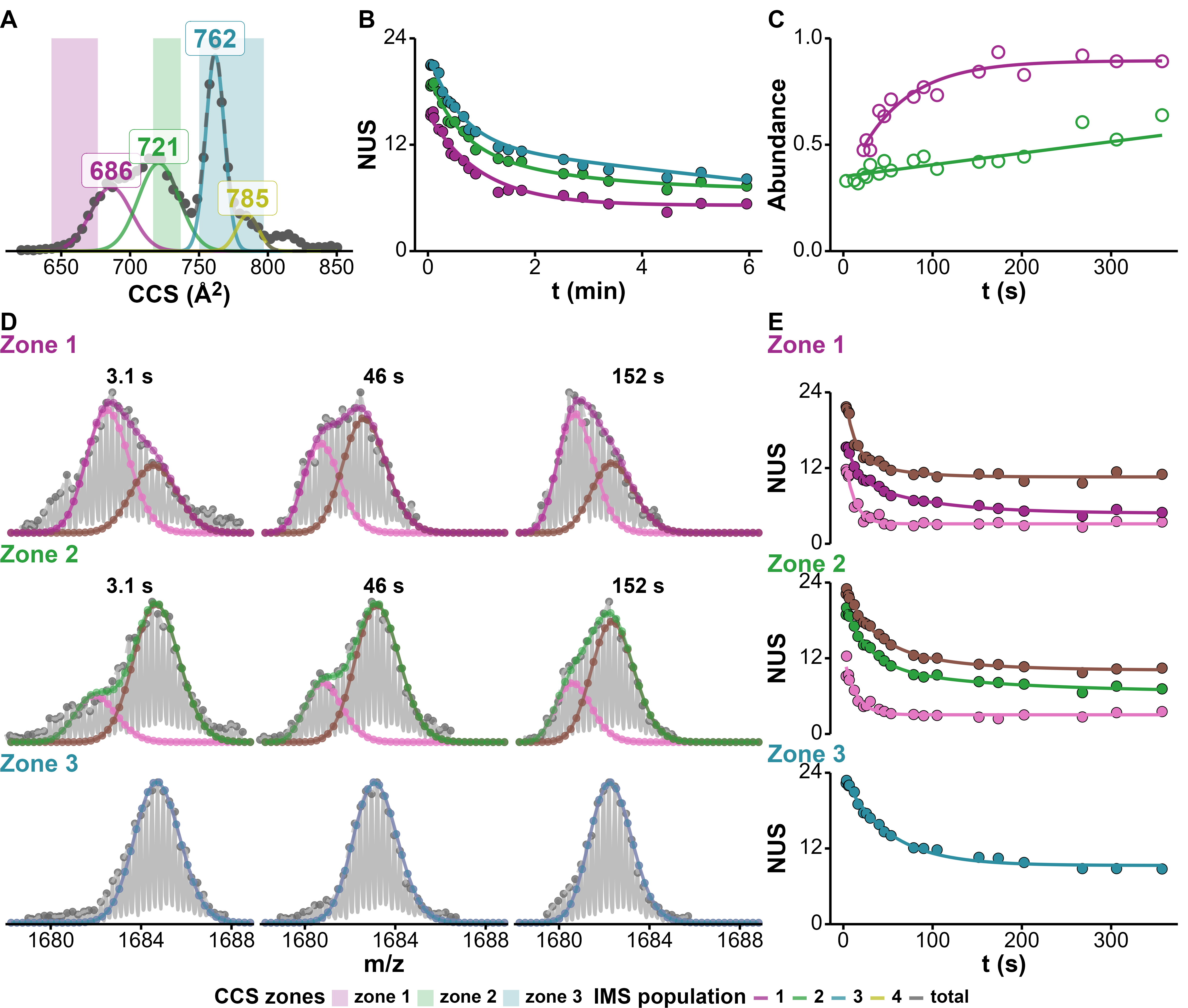
Cette approche a été utilisée pour un système encore plus complexe, le variant télomérique 5YEY, qui forme au moins quatre conformères dans nos conditions, dont trois ont la même masse (Figure 5.10). À l’instar de 23TAG, ces trois conformères de même masse échangent à des vitesses distinctes à cause de leurs tendances respectives à échanger par EX1.

Figure 5.10. Détection et caractérisation de conformères mineurs de 5YEY par HDX/IMS-MS native. A. Distributions de CCS de 5YEY·2K⁺ en présence de 1 mM de KCl. B. Cinétiques d’échange apparentes de trois zones IMS, définies dans le panneau A. Les distributions isotopiques de ces trois zones ont été déconvoluées (D), ce qui permet de quantifier leur échange par EX2 (E) et EX1 (C ; zones 1 et 2). On note ici que le conformère de la zone 3 échange purement par EX2, plus lentement que ceux des zones 1 et 2, qui échangent significativement par EX1.

5.2.1.3.2 Cas 2 : Plusieurs conformères en solution, de masses et CCS distinctes, et de même CCS et cinétiques d’échange

Il s’agit ici de filtrer les adduits non spécifiques, fréquents en ESI-MS native. Un seul exemple est déjà publié, où l’on s’intéresse à des complexes non-covalents de protéines [8]. Dans le cas des G4s, un oligonucléotide formant des conformères à 2 tétrades (“2T”) et 3 tétrades (“3T”) coordonne spécifiquement 1 et 2 K⁺, respectivement et ont donc des masses distinctes (MK et MK2, respectivement; Figure 5.11A,B). Cependant, 2T peut coordonner un potassium supplémentaire, non spécifiquement, et ainsi avoir la même masse que 3T. L’IMS permet de les séparer en phase gazeuse, et ainsi d’accéder à la cinétique d’échange “pure” de 3T (Figure 5.11C). De même pour 2T, on peut filtrer la contribution des brins non structurés (“U”). L’exemple de la Figure 5.11 illustre cette approche pour l’oligonucléotide 222T, qui forme des conformères U, 2T et 3T. Les distributions isotopiques observées pour MK2 sont particulièrement complexes, puisque 3T échange par EX2 et EX1 et que MK2 contient également un contaminant à 2 tétrades. On obtient donc une distribution trimodale, dont deux populations isotopiques sont corrélées (EX1 de 3T), et une indépendante (contaminant non spécifique de 2T) (Figure 5.11D, zone 2). La séparation IMS permet d’accéder aux contributions de 3T uniquement, et en particulier à son échange significatif par EX1 (Figure 5.11D, zone 3).

8. Hossain, B.M. et Konermann, L. Pulsed Hydrogen/Deuterium Exchange MS/MS for Studying the Relationship between Noncovalent Protein Complexes in Solution and in the Gas Phase after Electrospray Ionization. Analytical Chemistry, 2006, 78, 1613.

Figure 5.11. Filtrage des adduits non spécifiques de 222T par IMS : A. La présence d’adduits K⁺ non spécifiques produit des espèces de différentes conformations (U : non structuré, 2T : G4s à 2 tétrades, 3T : G4s à 3 tétrades) mais de même m/z : ici, 2T lié à un cation spécifique et un non spécifique (2T∙(1+1)K⁺) et U lié à deux cations non spécifiques (U∙(0+2)K⁺) ont le même m/z que 3T∙2K⁺ et sont donc mélangés dans MK2. Il en va de même pour MK qui contient 2T∙1K⁺ et U∙(0+1)K⁺. Notons que les structures présentées ici pour 222T ne sont pas connues et qu’il s’agit probablement de mélanges de conformères. B. Contour plot HDX/IMS-MS de 222T dans 0.1 mM KCl (en haut : spectre de masse natif, à droite : distribution des temps d’arrivée). C. L’extraction de régions IMS-MS spécifiques (rectangles colorés dans le panneau B) fournit les cinétiques d’échange apparentes des espèces 3T∙2K⁺ et 2T∙1K⁺ sans les contributions non spécifiques initialement présentes dans MK2 et MK, respectivement. D. La déconvolution de la distribution isotopique multimodale pour des temps d’échange sélectionnés met en évidence la présence d’un contaminant dans la zone 2 (vert ; distribution trimodale) de MK2 qui est filtré dans la zone 3 (bleu clair ; distribution bimodale).

5.2.1.3.3 Cas 3 : Même masses et cinétiques d’échanges mais CCS distinctes

Il y a en fait ici deux possibilités :

• Les pics distincts en mobilité ionique sont la conséquence de réarrangements entre la source (où la charge de l’analyte est acquise) et le tube de mobilité (Figure 5.9A). La cinétique d’échange en solution (avant l’ESI) n’est donc pas altérée. Dans ce cas de figure, l’HDX renseigne sur les mécanismes de réarrangement en phase gazeuse et permet de mieux comprendre certains résultats d’IMS-MS.

• Il y a des conformations distinctes en solution qui ont le même comportement HDX à l’échelle de temps où l’expérience est conduite. C’est sans doute le cas de conformères ayant le même cœur G4 (même nombre de tétrades et topologie) mais des structurations et dynamiques de boucles différentes. Notre approche méthodologique permet de sonder l’échange de la seconde à plusieurs jours, ce qui permet de voir les sites des tétrades échanger, mais pas ceux des boucles. Ici c’est l’IMS qui permet de mieux interpréter les résultats HDX, et en particulier permet de détecter des conformations alternatives qui n’impactent pas les cinétiques apparentes d’échange.

5.2.1.3.4 Conclusion

Cette approche combinant HDX en solution et IMS-MS native de biomolécules intactes est peu utilisée. Nous montrons ici qu’elle fonctionne avec des G4s, et que chaque technique, HDX et IMS, permet de mieux comprendre et interpréter les résultats de l’autre. Cette approche est potentiellement utile pour d’autres macromolécules de relativement bas poids moléculaires, pour lesquelles plusieurs conformères pourraient être séparés par IMS (assemblages supramoléculaires, peptidomimétiques, et assemblages protéiques conçus de novo [9]). Un exemple d’utilisation d’HDX/IMS-MS native sur des protéines est donnée dans la Section 5.2.2.

9. Lutz, I.D., Wang, S., Norn, C., Courbet, A., Borst, A.J., Zhao, Y.T., Dosey, A., Cao, L., Xu, J., Leaf, E.M., Treichel, C., Litvicov, P., Li, Z., Goodson, A.D., Rivera-Sánchez, P., Bratovianu, A.-M., Baek, M., King, N.P., Ruohola-Baker, H., et al. Top-down design of protein architectures with reinforcement learning. Science, 2023, 380, 266.

5.2.1.4 Etude de complexes G4/petites molécules

L’étude de l’interaction entre ligands et G4s à relativement haut débit (plusieurs complexes par jour) repose généralement sur des méthodes spectroscopiques : UV-melting, FRET-melting, dichroïsme circulaire, G4-FID (voir Section 1.4) [10]. Lorsque le système s’y prête, la structure des complexes formés peut être déterminée par RMN ou cristallographie. Ces techniques sont parfois limitées par le polymorphisme des analytes (ADN libre vs complexé, différentes topologies, différentes stœchiométries, etc.) et ne donne souvent accès qu’à un « instantané ». Le couplage entre HDX en solution, qui informe sur la dynamique ce ces espèces en solutions, et de la spectrométrie de masse native, qui permet de séparer ces espèces par masse et structure, est prometteur pour aller au-delà de ces instantanés [3].

10. Murat, P., Singh, Y. et Defrancq, E. Methods for investigating G-quadruplex DNA/ligand interactions. Chemical Society Reviews, 2011, 40, 5293.

Il s’agit d’une autre partie importante des travaux de thèse de Matthieu Ranz, assisté de Clarisse Fourel (Étudiante ingénieure, ENSMAC, Bordeaux) au départ de ce projet. Clarisse est maintenant en thèse sous la direction d’Ewen Lescop et Laurent Catoire (ICSN, Université Paris Saclay).

Nous avons sélectionné plusieurs ligands avec divers modes d’interaction qui induisent, ou non, des altérations structurales de l’ADN G4. Cela permettra de déterminer quelles informations peuvent en effet être collectées par HDX/MS. Nous appliquerons ensuite cette approche à des systèmes complexes dont le mode d’interaction n’est pas encore élucidé.

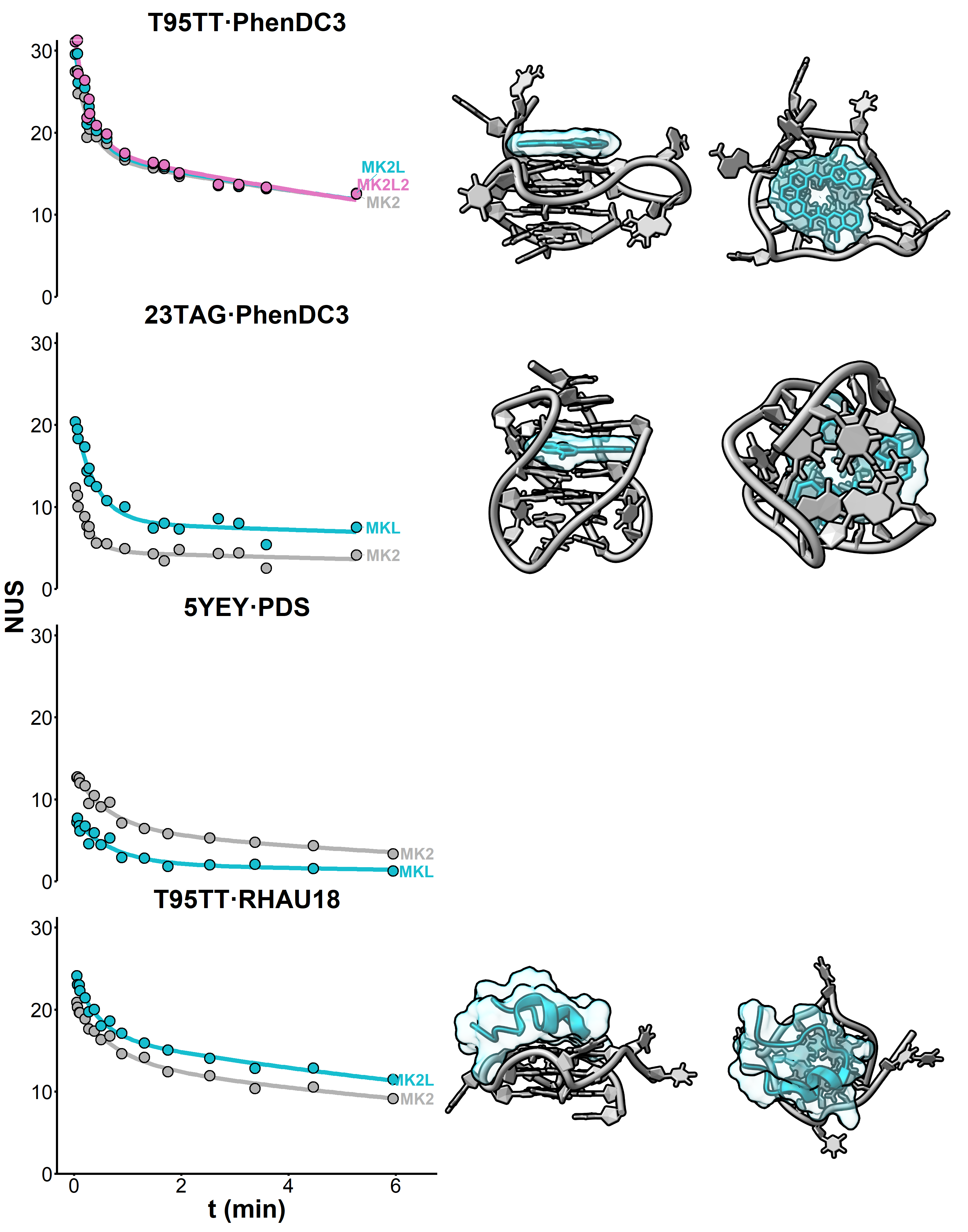
Nos premiers résultats montrent que les ligands interagissant par \(\pi\)-stacking sur les tétrades externes induisent un ralentissement de la cinétique d’échange dans les premières secondes/minutes par rapport au G4 libre, puis convergent vers des valeurs similaires (Figure 5.12; T95TT/PhenDC3). Cela s’explique par une protection accrue des tétrades externes, qui échangent normalement dans les premières secondes à minutes, mais pas des internes.

En revanche, lorsque l’échange induit un changement de conformation du G4, la cinétique d’échange est altérée sur l’ensemble des temps d’incubation, traduisant un changement de protection à l’échange de l’ensemble des sites. Dans le cas de 23TAG, l’intercalation de PhenDC3 induit un changement conformationnel qui augmente la protection de nombreux sites (Figure 5.12; 23TAG/PhenDC3). L’intercalation induit également la “perte” d’un potassium, ce qui peut être directement quantifié sur les spectres de masse native acquis pendant les expériences HDX. À l’inverse, l’interaction de PDS avec 5YEY mène à une déprotection globale du G4, qui peut être le résultat d’un déplacement de l’équilibre vers un G4 à deux tétrades (Figure 5.12; 5YEY/PDS).

Figure 5.12. Comparaison des cinétiques d’échanges de complexes G4/petites molécules (PhenDC3, PDS) et G4/peptide (RHAU18) et des G4s libres correspondant. À droite, les structures montrent le mode d’interaction attendu pour T95TT/PhenDC3 (PDB: 2MGN ; le G4 est c-myc dans cette structure), 23TAG/PhenDC3 (PDB: 2MGN) et T95TT/RHAU18 (PDB: 2N21).

D’autre part, l’analyse des distributions isotopiques a permis de montrer que le mécanisme d’échange EX1 est souvent inhibé en présence de ligand (cas de PhenDC3/23TAG), mais pas systématiquement (cas de PhenDC3/TBA), ce qui suggère que certains ligands se coordonnent de façon très dynamique.

Un point faible de cette approche est la dilution nécessaire au déclenchement de l’échange, ici d’un facteur 10. Dans le cas de complexes avec des \(K_d\) submicromolaires, cela n’a virtuellement aucune incidence. En revanche, lorsque le \(K_d\) est dans l’ordre de grandeur des analytes (5–10 \(\mu\)M), alors l’échange a lieu hors équilibre. Cela signifie qu’une partie du complexe peut se dissocier, et donc que les cinétiques mesurées pour l’ADN libre sont potentiellement “polluées” par des molécules d’ADN ayant partiellement échangées sous forme de complexe. Ce potentiel de contamination dépend de la cinétique de dissociation : si celle-ci est lente par rapport à la cinétique d’échange, alors l’incidence est faible. En revanche, dans le cas de dissociations rapides, la contamination peut être significative. Cela entraîne une différence apparente de cinétiques entre ADN libre et lié plus faible qu’elle ne devrait l’être. Une de mes perspectives à long terme est de mesurer les \(k_{off}\) et \(k_{on}\) des complexes étudiés en masse native avec une technique orthogonale comme la SPR ou le BLI.

Enfin, nous avons étendu notre gamme de ligands à un peptide, comme preuve de concept de cette approche pour étudier des complexes acides nucléiques / protéines. Le peptide RHAU18 interagit avec les tétrades terminales de l’aptamère G4 T95TT, sans changement conformationnel de ce dernier. Malgré cela, les cinétiques d’échange ne convergent pas comme dans les cas de \(\pi\)-stacking. Notre hypothèse est que le peptide protège partiellement la tétrade interne par interaction de l’extrémité C-terminale (en particulier K17 et Q18) dans le sillon du G4, mais il ne faut pas exclure d’éventuelles contributions de sites protégés sur le peptide lui-même. Pour cela, nous devrons étudier l’échange du peptide, et à terme de la protéine entière, par HDX/MS bottom-up “classique”, tel que décrit dans la Section 4.4.

L’HDX/MS semble donc avoir un excellent potentiel pour caractériser différents modes d’interaction et la dynamique des complexes formés. De plus, cette approche bénéficie des avantages de la spectrométrie de masse native, à savoir la détection et quantification des différentes stœchiométries en oligonucléotides, cations et ligands, et la détermination des \(K_d\) pour ces espèces séparées en masse, voire en IMS. Ces travaux, feront l’objet d’une publication avec Matthieu Ranz comme premier auteur.

5.2.1.5 Perspectives

Deux axes de travail se dégage désormais. Le premier est méthodologique, et consiste en l’identification d’une méthode de fragmentation en phase gazeuse des analytes, sans générer de réarrangement des isotopes (scrambling [11–17]) qui ferait perdre l’information acquise en solution. Cette approche top-down permettrait l’obtention des cinétiques d’échange à l’échelle d’un petit nombre de résidus, voire même d’un résidu unique, en plus de celles mesurées à l’échelle de l’analyte intact. Ces cinétiques résolus sur la séquence permettrait de déterminer quelles bases sont impliquées dans des motifs structuraux (paires de bases, tétrades) et des interactions non covalentes avec des ligands, du cation à la protéine.

11. Ferguson, P.L., Pan, J., Wilson, D.J., Dempsey, B., Lajoie, G., Shilton, B. et Konermann, L. Hydrogen/Deuterium Scrambling during Quadrupole Time-of-Flight MS/MS Analysis of a Zinc-Binding Protein Domain. Analytical Chemistry, 2006, 79, 153.

17. Anacleto, J., Kabir, E., Blanco, M., Leblanc, Y., Lento, C. et Wilson, D.J. Efficient, Zero Scrambling Fragmentation of Deuterium Labeled Peptides on the ZenoToF 7600 Electron Activated Dissociation Platform. Journal of the American Society for Mass Spectrometry, 2025, 36, 1175.

Le second axe de travail consiste à utiliser notre boîte à outils méthodologiques (résolution en temps de mélange, masse, conformation et séquence) pour étudier des complexes acides nucléiques/protéines. L’HDX/MS pourra aussi être appliqué au partenaire protéique, offrant une caractérisation complète des dynamiques d’interactions des deux partenaires. Explorer d’autres structures secondaires d’ADN et d’ARN (pas encore étudié du tout !) est également au programme, notamment en exploitant la séparation IMS.

Enfin, tangentiellement à ce projet, j’ai rejoint Carmelo Di Primo (ARNA) sur une étude fondamentale de l’utilisation du BLI pour étudier la structuration et les interactions d’oligonucléotides. À terme, j’aimerais inclure cette technique comme méthode orthogonale de mesures de cinétiques d’association et dissociation intra- et intermoléculaires.

5.2.2 HDX/MS native de protéines thérapeutiques

L’échange hydrogène-deutérium ne s’est pas cantonné aux acides nucléiques dans l’équipe BALI. J’ai ainsi modestement participé à un Projet financé par la Région Nouvelle Aquitaine, en collaboration avec la société Merck, qui utilise l’échange hydrogène-deutérium couplé à la spectrométrie de mobilité ionique et la spectrométrie de masse native pour l’étude de protéines thérapeutiques qui présentent des conformations multiples en solution. Ce projet, innovant techniquement, a permis de déterminer les conditions optimales de production et conservation de ces protéines, identifier les conformères actifs, et participera à la protection de la propriété intellectuelle.

D’un point de vue académique, ces travaux principalement menés par une chercheuse postdoctorante, Nina Khristenko (Figure 5.1), nous ont permis de découvrir un nouveau mécanisme d’ionisation des protéines par électrospray en conditions natives (Figure 5.13A) [18]. Durant ce projet, j’ai coencadré Nina en apportant mon expertise en HDX/MS et développement de méthodes analytiques pour la conception et la réalisation des expériences, le traitement de données, et l’interprétation des résultats.

18. Khristenko, N., Rosu, F., Largy, E., Haustant, J., Mesmin, C. et Gabelica, V. Native Electrospray Ionization of Multi-Domain Proteins via a Bead Ejection Mechanism. Journal of the American Chemical Society, 2023, 145, 498.

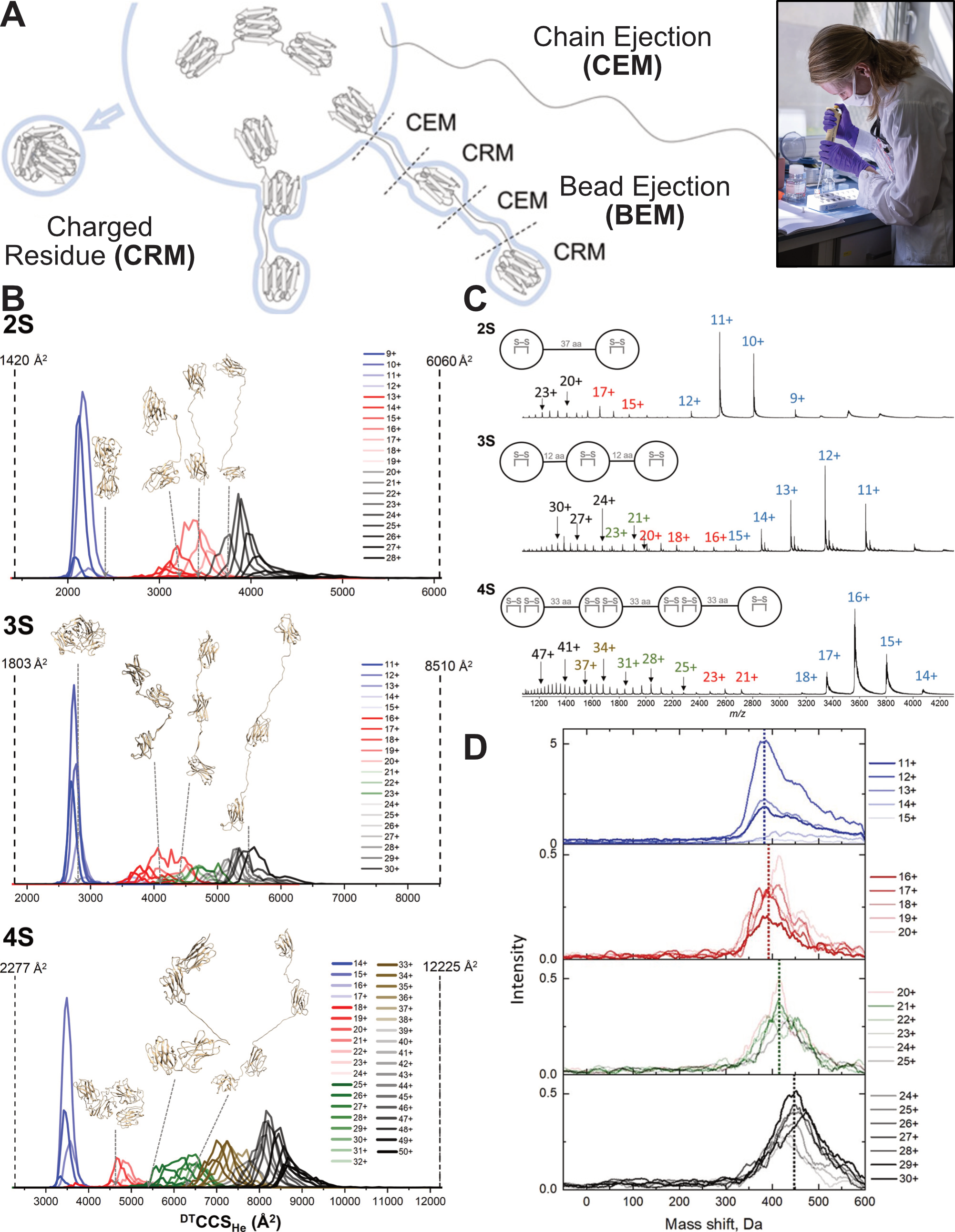
Plus spécifiquement, nous nous sommes intéressés à la structure en phase gazeuse de protéines thérapeutiques multi-domaines, constituées de domaines globulaires reliés par des régions non structurées. Leurs distributions de charges (masse native) et de sections efficaces de collision (IMS) sont multimodales (Figure 5.13B, C), ce qui suggère l’existence de plusieurs conformations en solution suivant des mécanismes d’ionisation distincts. Nous avons confirmé la présence de plusieurs conformations en solution (et non seulement en phase gazeuse) par HDX, en reprenant l’approche en flux continu développée pour les acides nucléiques, c’est à dire en conditions natives et à l’échelle de la protéine intacte, plutôt que par approche bottom up (Figure 5.13D). Les états de charge les plus élevées, correspondant aux CCS de protéines les plus allongées sont théoriquement les moins protégés de l’échange, ce qui est en effet ce que nous avons observé.

Le mécanisme d’ionisation électrospray est intrigant : une fraction de la population ne suit pas le mécanisme des résidus chargés (CRM) mais ne peut pas non plus s’ioniser par pure éjection de chaîne. Nous en avons déduit qu’un mécanisme hybride est possible, dans lequel les domaines globulaires sont éjectés un à la fois d’une gouttelette mère. Les corrélations entre la charge et la surface accessible au solvant de protéines dénaturées ou intrinsèquement désordonnées sont également compatibles avec ce “mécanisme d’éjection de perles” (BEM), que nous avons proposé comme principe général de l’électrospray des biomolécules.

Figure 5.13. Ionisation en ESI natif de protéines multidomaines. A. Illustration des mécanismes coexistant proposés : le CRM produit un ensemble globulaire, chargé à un niveau proche de la limite de Rayleigh. Le CEM produit une conformation entièrement étendue. Le BEM est intermédiaire parce qu’il est un composite du CRM et du CEM : les domaines structurés peuvent être ionisés par le CRM tandis que les régions désordonnées peuvent être ionisées par le CEM. Encart : Nina Khristenko B. Distribution de CCS des protéines 2S, 3S et 4S en fonction de leurs états de charge. Les segments verticaux hachurés représentent les valeurs estimées de CCS si ces protéines étaient parfaitement globulaires (valeurs basses) ou complètement allongées (valeurs hautes). C. Spectres de masse native des protéines 2S, 3S et 4S. D. Déplacement du centroïde de masse de la protéine 3S après 53 s d’HDX en solution, en fonction des états de charge.

5.3 Ligands de G4s

5.3.1 Ligands capables de discriminer des topologies G4

Après plusieurs années sans opportunités de pouvoir jouer avec des ligands de G4, j’ai enfin eu l’opportunité de revenir à mes premières amours. Comme évoqué précédemment, une petite molécule pouvant se lier spécifiquement à un seul G4 permettrait de potentiellement réguler des processus biologiques avec peu d’effets secondaires liées aux interactions avec l’ADN duplex. Lors de ma thèse, j’ai développé une méthode permettant d’évaluer la sélectivité de ligands pour des structures G4s distinctes, mais ai dû faire le constat qu’il n’était pas encore possible de concevoir rationnellement un ligand ciblant une structure G4 particulière (Sections 1.4.1.1, 1.4.1.2.1) [19, 20]. Nous avons synthétisé des molécules capables de discriminer très efficacement certaines topologies, mais sans pouvoir complètement rationaliser ces effets (Section 1.3.2) [21, 22]. Je m’en suis donc remis au criblage, mais sans découvrir de design moléculaire radicalement différent (Section 1.4.1.2.2) [23].

19. Largy, E., Hamon, F. et Teulade-Fichou, M.-P. Development of a high-throughput G4-FID assay for screening and evaluation of small molecules binding quadruplex nucleic acid structures. Analytical and Bioanalytical Chemistry, 2011, 400, 3419.

20. Tran, P.L.T., Largy, E., Hamon, F., Teulade-Fichou, M.-P. et Mergny, J.-L. Fluorescence intercalator displacement assay for screening G4 ligands towards a variety of G-quadruplex structures. Biochimie, 2011, 93, 1288.

21. Hamon, F., Largy, E., Guédin-Beaurepaire, A., Rouchon-Dagois, M., Sidibe, A., Monchaud, D., Mergny, J.-L., Riou, J.-F., Nguyen, C.-H. et Teulade-Fichou, M.-P. An Acyclic Oligoheteroaryle That Discriminates Strongly between Diverse G-Quadruplex Topologies. Angewandte Chemie International Edition, 2011, 50, 8745.

22. Petenzi, M., Verga, D., Largy, E., Hamon, F., Doria, F., Teulade-Fichou, M.-P., Guédin, A., Mergny, J.-L., Mella, M. et Freccero, M. Cationic Pentaheteroaryls as Selective G-Quadruplex Ligands by Solvent-Free Microwave-Assisted Synthesis. Chemistry A European Journal, 2012, 18, 14487.

23. Largy, E., Saettel, N., Hamon, F., Dubruille, S. et Teulade-Fichou, M.-P. Screening of a Chemical Library by HT-G4-FID for Discovery of Selective G-quadruplex Binders. Current Pharmaceutical Design, 2012, 18, 1992.

24. Berner, A., Das, R.N., Bhuma, N., Golebiewska, J., Abrahamsson, A., Andréasson, M., Chaudhari, N., Doimo, M., Bose, P.P., Chand, K., Strömberg, R., Wanrooij, S. et Chorell, E. G4-Ligand-Conjugated Oligonucleotides Mediate Selective Binding and Stabilization of Individual G4 DNA Structures. Journal of the American Chemical Society, 2024, 146, 6926.

25. Qin, G., Liu, Z., Yang, J., Liao, X., Zhao, C., Ren, J. et Qu, X. Targeting specific DNA G-quadruplexes with CRISPR-guided G-quadruplex-binding proteins and ligands. Nature Cell Biology, 2024, 26, 1212.

26. Kumar, S., Pany, S.P.P., Sudhakar, S., Singh, S.B., Todankar, C.S. et Pradeepkumar, P.I. Targeting Parallel Topology of G-Quadruplex Structures by Indole- Fused Quindoline Scaffolds. Biochemistry, 2022, 61, 2546.

27. Cheng, A., Liu, C., Ye, W., Huang, D., She, W., Liu, X., Fung, C.P., Xu, N., Suen, M.C., Ye, W., Sung, H.H.Y., Williams, I.D., Zhu, G. et Qian, P.-Y. Selective C9orf72 G-Quadruplex-Binding Small Molecules Ameliorate Pathological Signatures of ALS/FTD Models. Journal of Medicinal Chemistry, 2022, 65, 12825.

28. Wang, R. et Hu, M.-H. Development of a fluorescent ligand that specifically binds to the c-MYC G-quadruplex by migrating the benzene group on a carbazole-benzothiazolium scaffold. Bioorganic Chemistry, 2024, 151, 107690.

29. Long, W., Zheng, B.-X., Li, Y., Huang, X.-H., Lin, D.-M., Chen, C.-C., Hou, J.-Q., Ou, T.-M., Wong, W.-L., Zhang, K. et Lu, Y.-J. Rational design of small-molecules to recognize G-quadruplexes of c-MYC promoter and telomere and the evaluation of their in vivo antitumor activity against breast cancer. Nucleic Acids Research, 2022, 50, 1829.

30. Lu, X., Passalacqua, L.F.M., Nodwell, M., Kong, K.Y.S., Caballero-García, G., Dolgosheina, E., Ferré-D’Amaré, A., Britton, R. et Unrau, P. Symmetry breaking of fluorophore binding to a G-quadruplex generates an RNA aptamer with picomolar KD. Nucleic Acids Research, 2024, 10.1093/nar/gkae493.

De récentes études présentent des approches très prometteuses pour obtenir des sélectivités intra-G4 significatives [24, 25], mais beaucoup des sélectivités publiées dans la littérature se limitent à l’étude d’un nombre réduit de séquences que l’on pourrait qualifier de cherry picking. Un exemple récent, pris totalement au hasard, présente des ligands indo-quinolines comme sélectifs de topologies parallèles, mais seulement quatre séquences G4s (dont deux parallèles) et un contrôle duplex ont été testées [26]. Dans un autre exemple récent, les auteurs présentent trois molécules qui seraient sélectives d’un seul G4 (C9orf72) avec des \(K_d\) de 2–3 mM (oui, millimolaires) [27]. Troisième et dernier exemple aléatoire, où un dérivé de TO est présenté comme spécifique de c-MYC après comparaison avec trois G4s, sa faible sélectivité apparente étant cachée Supporting Information [28]. Le TO est d’ailleurs à la mode, puisque d’autres groupes ont modifié sa structure pour moduler son affinité et sa sélectivité [29, 30].

5.3.1.1 Ligands foldamères spécifiques des topologies parallèles

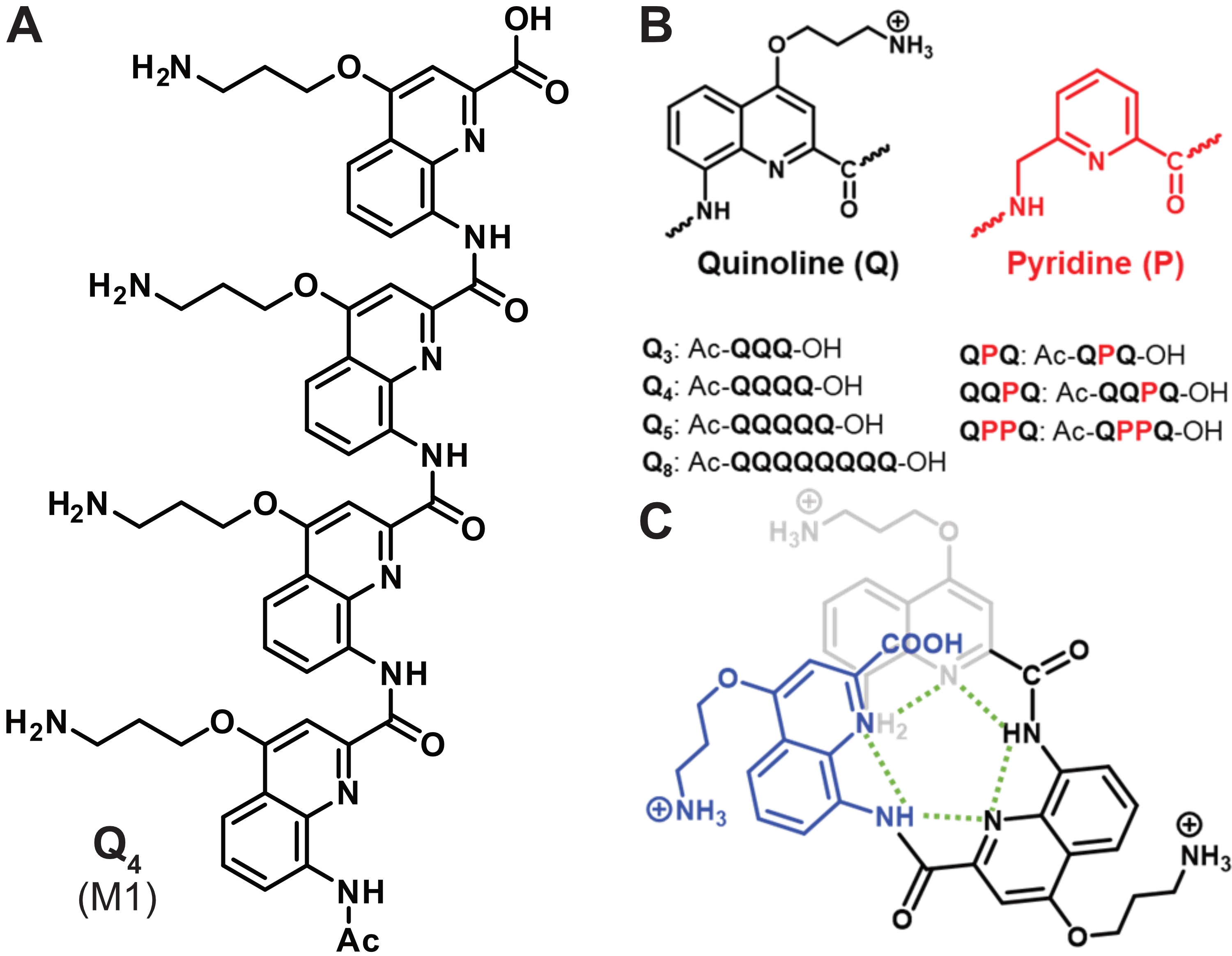
Lors de son séjour sabbatique dans l’équipe, Liliya Yatsunyk (Professeure à Swarthmore, PA, USA) a observé par ESI-MS la formation d’un complexe entre un G4 de c-myc et une molécule inconnue contaminant le spectromètre de masse. Après que Liliya a identifié le propriétaire de la molécule, l’équipe de Yann Ferrand (IECB, Bordeaux), et la nature de celle-ci, je me suis retrouvé le chanceux propriétaire du foldamère M1, plus tard rebaptisé Q₄ (Figure 5.14A).¹ Moore définit les foldamères comme “tout oligomère qui se replie dans un état conformationnel ordonné en solution, dont les structures sont stabilisées par un ensemble d’interactions non covalentes entre les unités monomères non adjacentes” [31]. Il existe deux grandes classes de foldamères : les foldamères à brin unique qui se replient uniquement sur eux-mêmes (peptidomimétiques) et les foldamères à brin multiple qui peuvent également s’associer (nucléotidomimétiques). Ici, c’est de la première que j’hérite, puisque Q₄ fait partie d’une série de foldamères formés d’hétérocycles pyridine (P) et quinoline (Q) liés par des amides, ce qu’un cerveau contaminé par les ligands de G4s pourrait aussi interpréter comme des oligomères de 360A (Figure 1.6).

¹ D’où l’intérêt de tenir à jour les log books des instruments.

31. Hill, D.J., Mio, M.J., Prince, R.B., Hughes, T.S. et Moore, J.S. A Field Guide to Foldamers. Chemical Reviews, 2001, 101, 3893.

De fait, ces foldamères possèdent deux caractéristiques classiques des ligands de G4 :

1. une structure basée sur des hétérocycles (Figure 5.14), bien que non condensés ici, à l’image de TOxaPy (Section 1.3.2)

2. Des chaînes latérales étendues et flexibles, pouvant potentiellement interagir dans les boucles et sillons des G4s. Ici chaque quinoline possède une chaîne latérale chargée positivement à pH physiologique, ce qui améliore la solubilité dans l’eau et permet de cibler les phosphates (Figure 5.14A, B).

La différence essentielle avec les ligands de G4s “classiques” réside dans le fait que ces foldamères ne sont pas plats, mais se replient en hélice grâce notamment à des des répulsions électrostatiques, des liaisons hydrogène intramoléculaires, une conjugaison et un empilement aromatique significatifs [32–34].

32. Jena, P.V., Shirude, P.S., Okumus, B., Laxmi-Reddy, K., Godde, F., Huc, I., Balasubramanian, S. et Ha, T. G-Quadruplex DNA Bound by a Synthetic Ligand is Highly Dynamic. Journal of the American Chemical Society, 2009, 131, 12522.

34. Mandal, P.K., Baptiste, B., Langloisd’Estaintot, B., Kauffmann, B. et Huc, I. Multivalent Interactions between an Aromatic Helical Foldamer and a DNA G-Quadruplex in the Solid State. ChemBioChem, 2016, 17, 1911.

Figure 5.14. Série de foldamères amidoquinolines. A. Le contaminant par lequel tout a débuté, initialement nommé M1 avant d’être rebaptisé Q₄. B. Les différents foldamères de la série dont l’affinité et la sélectivité pour les G4s ont été évaluées. C. Vue du dessus de l’extrémité C-terminale de l’hélice formée par cette famille de foldamères.

Avec Benjamin Liénard (stagiaire de licence, Bordeaux), nous avons confirmé l’interaction forte entre Q₄ et c-myc, mais également découvert que ce ligand a une préférence marquée pour certaines séquences, sans toutefois caractériser cette sélectivité complètement, ni en déterminer l’origine.

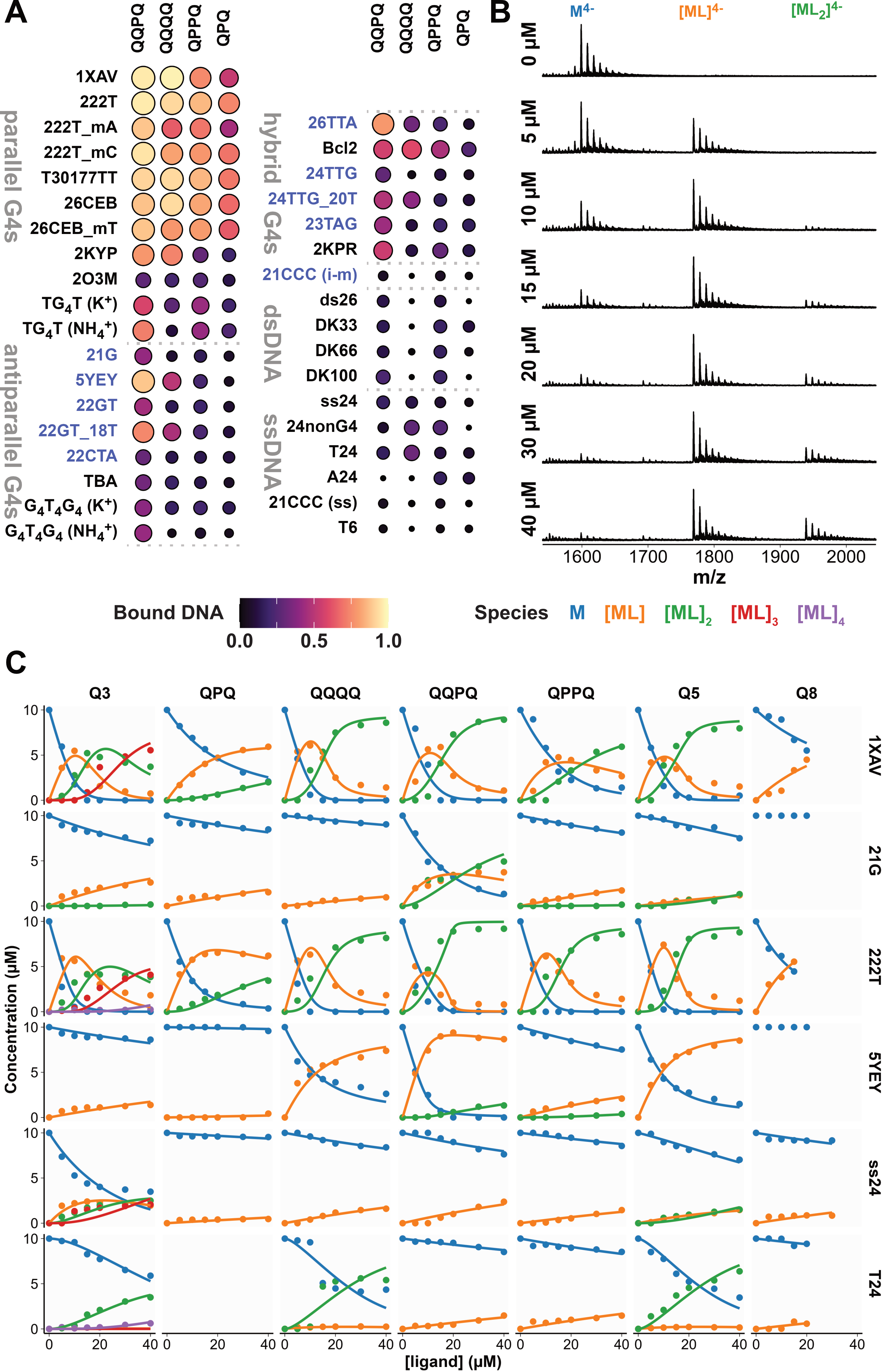
Grâce au coencadrement doctoral d’Alexander König, j’ai pu réexplorer ce thème de recherche pour tenter d’enfin sortir du paradigme du ligand aromatique plan condensé. Vincent Laffilé, doctorant de l’équipe de Y. Ferrand, a synthétisé une série de ces foldamères (Figure 5.14B), nous permettant de mieux caractériser les déterminants de cette sélectivité. Surtout, Alexander a souhaité tester un large panel de structures secondaires pour éviter les conclusions hâtives sur ladite sélectivité. Il a ainsi criblé par spectrométrie de masse native une large gamme de G4s et de contrôles non-G4, ce qui a permis de mettre en évidence la préférence marquée de QQPQ, Q₄, QPPQ et QPQ pour la topologie parallèle (Figure 5.15A).

Figure 5.15. Utilisation de la spectrométrie de masse native pour cribler une large gamme d’oligonucléotides avec des foldamères de synthèse. A. Heatmap de la fraction d’ADN lié par un équivalent molaire de foldamère. 21CCC est un i-motif. B. Exemple de spectres obtenus pour la titration de 222T avec QPQ (M = G4 monomérique, L = ligand foldamère). C. Titrations modélisées semi-automatiquement.

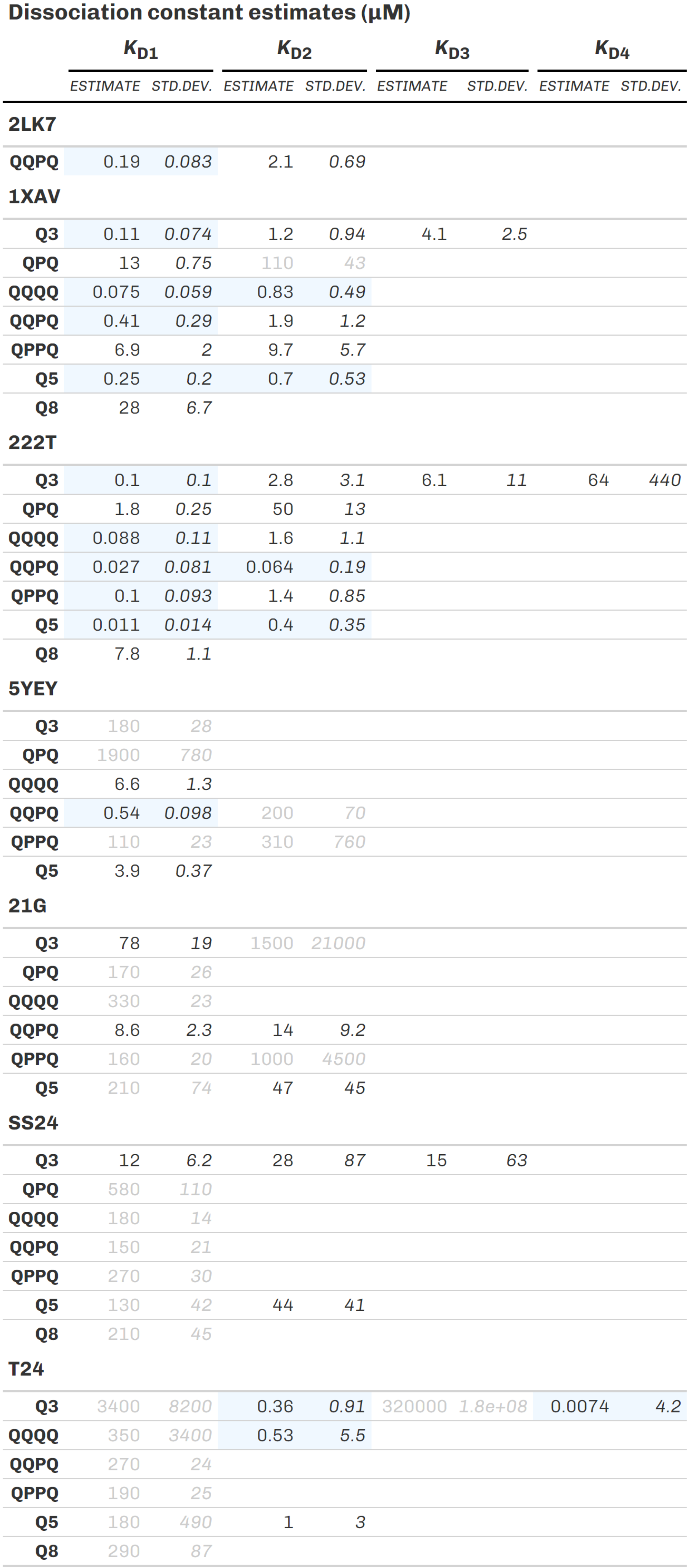
J’ai développé un script pour la quantification semi-automatisée de chacune des espèces (les différentes stœchiométries d’interaction) de ces 144 spectres de masse, et le calcul subséquent des affinités. J’ai également utilisé ce script pour quantifier les espèces des titrations entre sept foldamères et six oligonucléotides (294 spectres ; Figure 5.15B, C). J’ai ensuite écris un script générant… des scripts servant d’input pour le logiciel DynaFit, permettant la modélisation dynamique de ces titrations sur la base des équations chimiques de réactions [35, 36]. L’exécution de ces scripts automatiquement et l’extraction des résultats (\(K_d\), coopérativités, paramètres de fit) ont également été scriptées. Cette automatisation du traitement des données a permis un gain de temps notable et des gains de robustesse et répétabilité. Ces titrations ont permis la détermination de \(K_d\) de l’ordre de la centaine de nanomolaires pour les G4s parallèles, plusieurs ordres de grandeur de mieux qu’avec les autres topologies, bien que des exceptions existent (Figure 5.16).

35. Kuzmič, P. Program DYNAFIT for the Analysis of Enzyme Kinetic Data: Application to HIV Proteinase. Analytical Biochemistry, 1996, 237, 260.

36. Kuzmič, P. DynaFitA Software Package for Enzymology. In. 2009, Elsevier, p. 247‑280.

Figure 5.16. Constantes de dissociations des réactions successives de complexation des foldamères. Les constantes submicromolaires sont colorées en bleu. Bien que les foldamères ont généralement des affinités plusieurs ordres de grandeurs meilleurs avec les G4s parallèles (1XAV, 222T) qu’avec les hybrides/antiparallèles (5YEY, 21G) ou les simples brins déstructurés (ss24, T24), des exceptions existent. En particulier, QQPQ se lient très bien à 5YEY, et Q₃ et Q₄ se lient de façon coopérative - 2 par 2 ! - à T24.

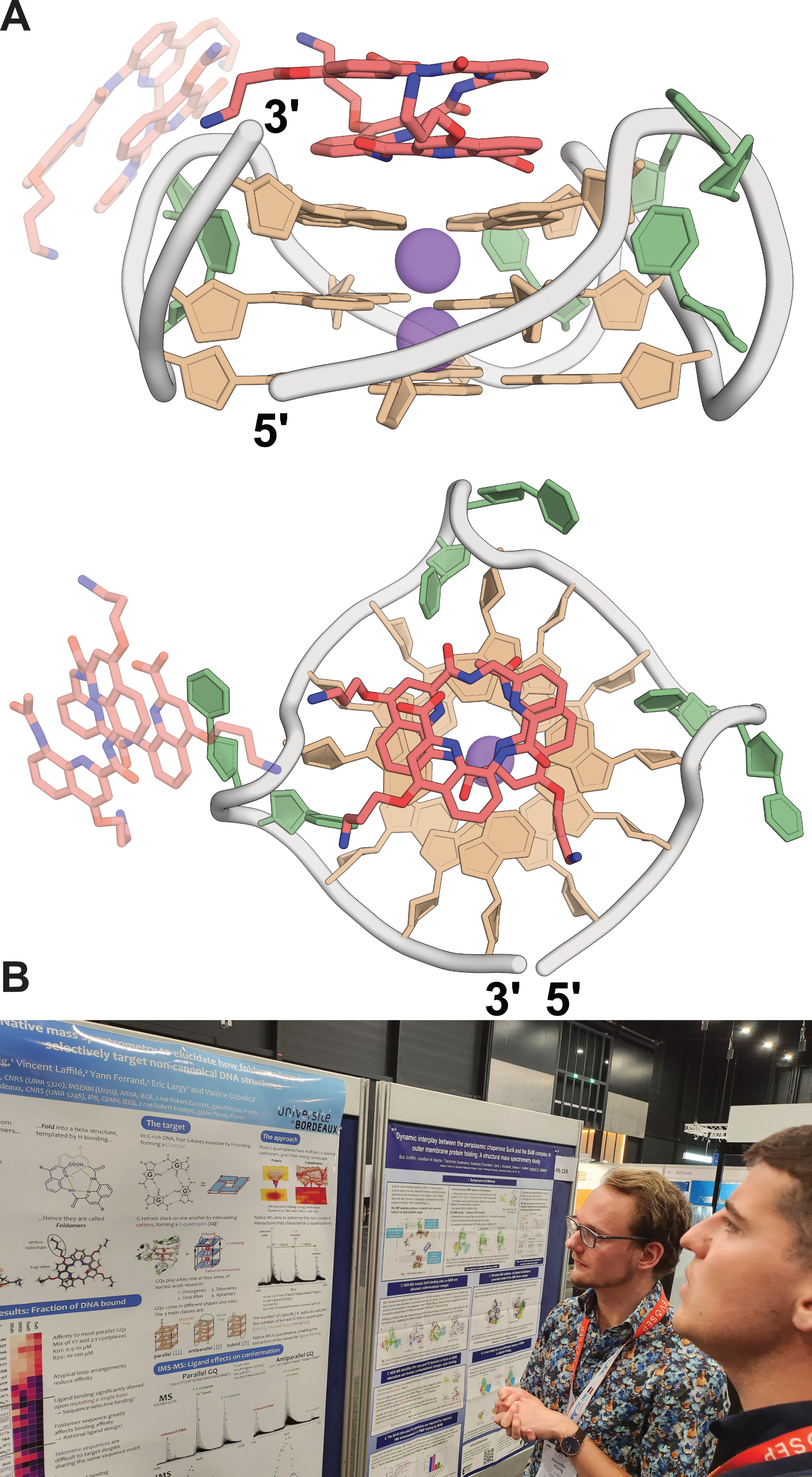
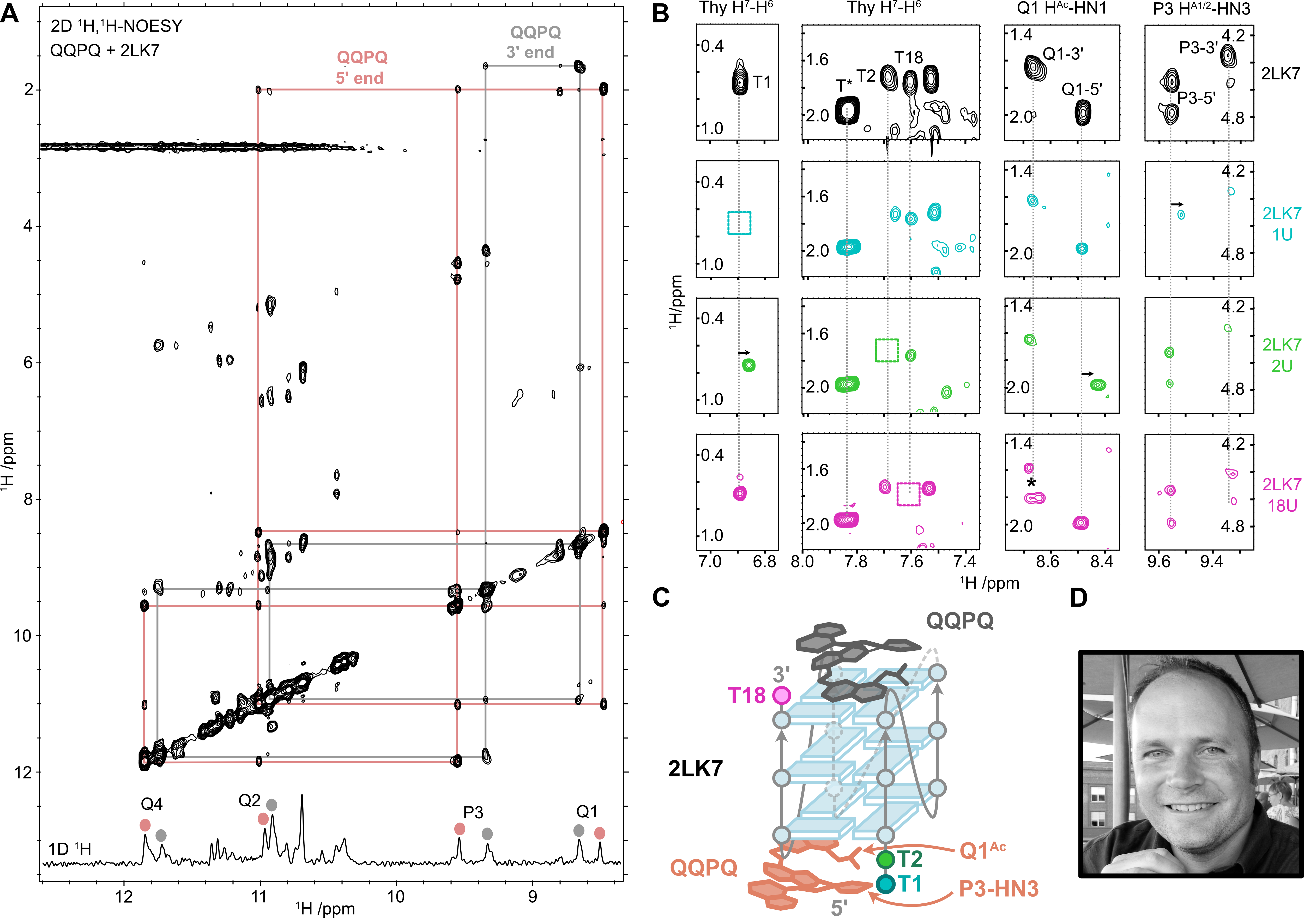
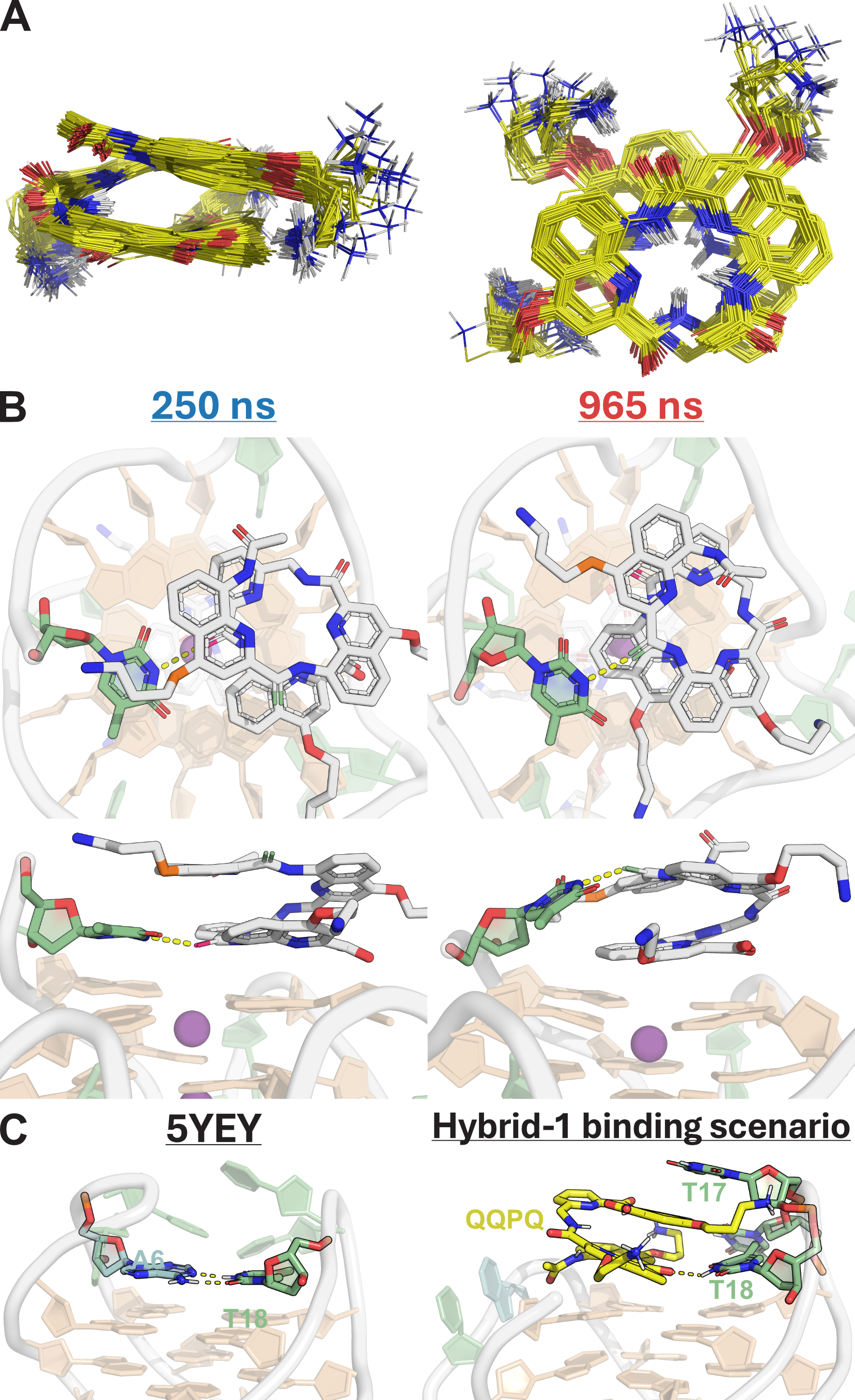
Nous avons également observé par dichroïsme circulaire que ces ligands peuvent induire des changements de conformations de G4s non parallèles, vers la topologie parallèle, confirmant cette nette préférence structurale. Afin d’élucider l’origine de cette préférence, nous avons tenté de cristalliser certains de ces complexes avec l’aide précieuse de Stéphane Thore (ARNA, équipe PRISM). Cela nous a permis de proposer une structure pour le complexe QQPQ/222T (Figure 5.17), que nous avons ensuite également étudié par RMN avec Cameron Mackereth (avec un G4 légèrement différent pour obtenir des pics iminos, marqueurs de la formation des tétrades, mieux résolus ; Figure 5.18).

Figure 5.17. A. Structure cristalline du complexe QPQQ/222T. On notera la présence d’un second site d’interaction du ligand qui permet des contacts dans le cristal et n’existe pas en solution. B. Alexander König présente ses résultats à l’International Mass Spectrometry Conference (IMSC), 27 août 2022, Maastricht (Pays-Bas).

Les deux approches montrent que l’interaction se fait par \(\pi\)-stacking sur les tétrades externes. Dans le cristal, seule une tétrade est coordonnée par le foldamère car le G4 dimérise via l’autre face. En solution, en revanche, nous avons mis en évidence que l’interaction se fait sur les deux faces, ce qui est cohérent avec les stœchiométries déterminées par spectrométrie de masse. Ce stacking est la norme des ligands de G4s. En revanche, cette hélice positionnée de façon coaxiale au canal ionique du G4 induit un encombrement stérique important au-dessus des tétrades. L’interaction est donc favorable lorsque ces tétrades sont relativement peu encombrées, comme dans les G4s parallèles. Dans les autres topologies, des boucles recouvrent les tétrades, rendant l’interaction stériquement peu favorable, bien que possible dans certains cas particuliers comme QPQQ/5YEY (Figure 5.16). Les données CD, MS et RMN supportent ici un réarrangement en un G4 hybride à trois tétrades, dont une seule présente un environnement favorable à l’interaction.

Figure 5.18. A. Spectre 2D ¹H,¹H-NOESY (temps de mélange de 200 ms) de 2LK7 (dTTG₃TG₃TG₃TG₃T ; 100 μM, tampon KP 10 mM, pH 7.0, dans 90/10 H₂O/D₂O) en présence de QQPQ (300 μM), montrant deux réseaux de corrélations NOE reliant les protons amide (NH) du foldamère. L’encart inférieur présente la région imino du spectre 1D annotée avec les signaux des deux espèces de foldamères. B) Régions sélectionnées du spectre ¹H,¹H-NOESY de QQPQ lié à 2LK7, et des mutants où un T est substitué par un U : 2LK7-1U, 2LK7-2U et 2LK7-18U, ayant permis d’identifier les sites d’interactions en 5’ et 3’. Les lignes verticales indiquent les déplacements chimiques d’origine des protons H5 de la thymine, du NH1 de Q1 et du NH3 de P3 du QQPQ. Les carrés mettent en évidence l’absence de signaux lorsque la thymidine est remplacée par la désoxyuridine. C. Schéma du complexe 2:1 QQPQ:2LK7, où le QQPQ est représenté en saumon et en gris pour les sites de liaison 5’ et 3’, respectivement. Les résidus T1, T2 et T18 sont colorés comme dans B. Encart : Cameron Mackereth.

Les densités électroniques assez diffusent de l’étude cristallographique, couplées à la relative symétrie de la molécule, ne permettent pas de conclure sur le mode d’interaction. Il est théoriquement possible pour le ligand d’être positionné dans la position inversée (vis-à-vis des extrémités N et C terminales) et de pouvoir pivoter autour de l’axe de l’hélice, ce qui expliquerait les densités électroniques diffuses.

J’ai donc appliqué le workflow de dynamiques moléculaires que j’ai mis en place à mon arrivée dans l’équipe de Cameron, détaillé dans la Section 5.6.2, en me basant sur la structure cristalline. J’ai préalablement vérifié que la conformation hélicoïdale de QQPQ est la seule pertinente par calculs de mécanique quantique (Figure 5.19A), et dérivé par la même méthode des paramètres modifiés de champs de force pour ce ligand. Les observations les plus importantes sur un conformère parallèle de 222T ont confirmé nos hypothèses :

• Deux QQPQ peuvent se stacker en 5’ et 3’, sans gêne stérique, sans perte d’hélicité du foldamère, et sans préférence notable pour un interaction via les extrémités N et C-terminales.

• Tous les modes d’interactions identifiés par analyse en composantes principales (PCA) et clustering des trajectoires MD présentent QQPQ positionné de façon décentrée par rapport à la tétrade, ce qui maximise les interactions \(\pi-\pi\) (Figure 5.19B).

• Les chaînes latérales peuvent se lier au squelette phosphate de façon transitoire et sont globalement très dynamiques, à l’instar des dT en 5’ et 3’, ce qui justifie leur absence dans le modèle cristallographique.

• QQPQ peut tourner autour de son axe hélicoïdal (Figure 5.19B), parfois en complétant une rotation complète en l’espace d’une microseconde de simulation, tout en maintenant des angles interplanaires optimaux pour le \(\pi\)-stacking.

• Les amides de QQPQ peuvent interagir de façon discrète avec des thymines de boucles (Figure 5.19B), venant confirmer la tendance de ces foldamères à lier des oligonucléotides riches en T. Cette interaction particulière a également été observé pour 5YEY (Figure 5.19C), amenant un élément d’explication de l’affinité particulièrement bonne de QQPQ pour ce G4 non parallèle dont la topologie est altérée par l’interaction.

Figure 5.19. A. Ensemble conformationnel de QQPQ. Vue latérale (gauche) et vue de dessus (droite) des 133 conformères identifiés et superposés par l’algorithme GOAT (Global Optimizer Algorithm) : Un premier minimum local est déterminé à partir de la position initiale sur la surface d’énergie potentielle. L’énergie est ensuite augmentée dans un champs de force (GFN-FF) jusqu’à franchir une barrière, puis une nouvelle optimisation de géométrie semi-empirique (GFN2-xTB) permet d’identifier un nouveau minimum. Le processus est répété jusqu’à ce qu’aucun nouveau minimum ne soit trouvé. B. Exemple de mode d’interaction discret de QQPQ impliquant une thymine à l’extrémité 5’ (liaison hydrogène entre O6 (rose) et le N3 de dT1 (250 ns), inhibant la rotation du foldamère. La disruption de cette interaction rétablit la liberté rotationnelle de QQPQ (droite, 965 ns). C. Structure publiée de 5YEY (gauche) [37], et un complexe QQPQ·5YEY de topologie hybrid-1, extrait aléatoirement de la simulation MD. Dans ce dernier, la paire de bases A6:T18 est rompue, laissant de l’espace au-dessus de la tétrade 5’ pour que QQPQ puisse se stacker. T18 est disponible pour se lier à l’oxygène de l’amide de l’extrémité N-terminale de QQPQ, qui est également stacké par T17 sà son extrémité C-terminale.

37. Liu, C., Zhou, B., Geng, Y., Yan Tam, D., Feng, R., Miao, H., Xu, N., Shi, X., You, Y., Hong, Y., Tang, B.Z., Kwan Lo, P., Kuryavyi, V. et Zhu, G. A chair-type G-quadruplex structure formed by a human telomeric variant DNA in K⁺solution. Chemical Science, 2019, 10, 218.

Ces travaux, récemment acceptés pour publication dans Nucleic Acids Res. avec Alexander König en premier auteur, nous permettent donc de proposer un nouveau paradigme pour la synthèse rationnelle de ligands capables de discriminer des topologies particulières de G4s : il est possible de concevoir des ligands sélectifs de G4s parallèles en associant une surface aromatique permettant le stacking à une structure tridimensionnelle non plane empêchant l’interaction avec les autres topologies. Cette approche avait déjà été explorée lors de ma thèse, et avant [38], avec des complexes métalliques incluant des ligands apicaux, mais la gène stérique associée était bien plus modeste qu’avec des foldamères. Les informations structurales générées par RMN et cristallographie seront très utiles pour optimiser rationnellement ces foldamères pour le ciblage spécifique de certaines topologies G4.

38. Bertrand, H., Monchaud, D., De Cian, A., Guillot, R., Mergny, J.-L. et Teulade-Fichou, M.-P. The importance of metal geometry in the recognition of G-quadruplex-DNA by metal-terpyridine complexes. Organic & Biomolecular Chemistry, 2007, 5, 2555.

Finalement, cette étude illustre le potentiel de la spectrométrie de masse native pour cribler et caractériser des ligands de G4 sans cherry picking et sa complémentarité avec des techniques structurales de plus hautes résolutions. Sur une note plus personnelle, je suis très friand d’études combinant plusieurs techniques orthogonales pour étudier un système d’intérêt, et je trouve très drôle qu’après des années à concevoir rationnellement ou cribler des ligands de G4s, on en trouve un par hasard.

5.3.1.2 Ligands pérylènes spécifiques d’une conformation intermédiaire de structuration de c-KIT2

Durant mes activités de caractérisation de ligands de G4 par spectrométrie de masse, j’ai également encadré Silvia Ceschi, une étudiante de thèse de l’université de Padoue (Figure 5.20C ; maintenant postdoc au Massachusetts General Hospital), lors de son séjour de 6 mois au laboratoire pour ses travaux sur la séquence KIT2 du promoteur d’oncogène humain c-KIT [39]. Plus précisément, l’étude était centrée sur la sélection d’un intermédiaire structuré en G4, à long temps de vie, pour lequel un rôle physiologique est possible compte tenu de la vitesse des processus transcriptionnels [40].

39. Fernando, H., Reszka, A.P., Huppert, J., Ladame, S., Rankin, S., Venkitaraman, A.R., Neidle, S. et Balasubramanian, S. A Conserved Quadruplex Motif Located in a Transcription Activation Site of the Human c-kit Oncogene. Biochemistry, 2006, 45, 7854.

40. Rigo, R., Dean, W.L., Gray, R.D., Chaires, J.B. et Sissi, C. Conformational profiling of a G-rich sequence within the c-KIT promoter. Nucleic Acids Research, 2017, 45, 13056.

Figure 5.20. A. Structures de PIPER et K20. B. Spectres de masse native de KIT* (0.01 mM) en présence d’un équivalent molaire de K20 ou PIPER, dans un tampon 100 mM TMAA, 4 mM KCl. On notera ici l’utilisation de quantités de KCl peu adaptées à la spectrométrie de masse native. Adapté avec permission [41]. C. L’équipe BALI en juillet 2019. De gauche à droite : Steven Daly, Silvia Ceschi, Federica D’Aria, Eric Largy, Valérie Gabelica, Frédéric Rosu.

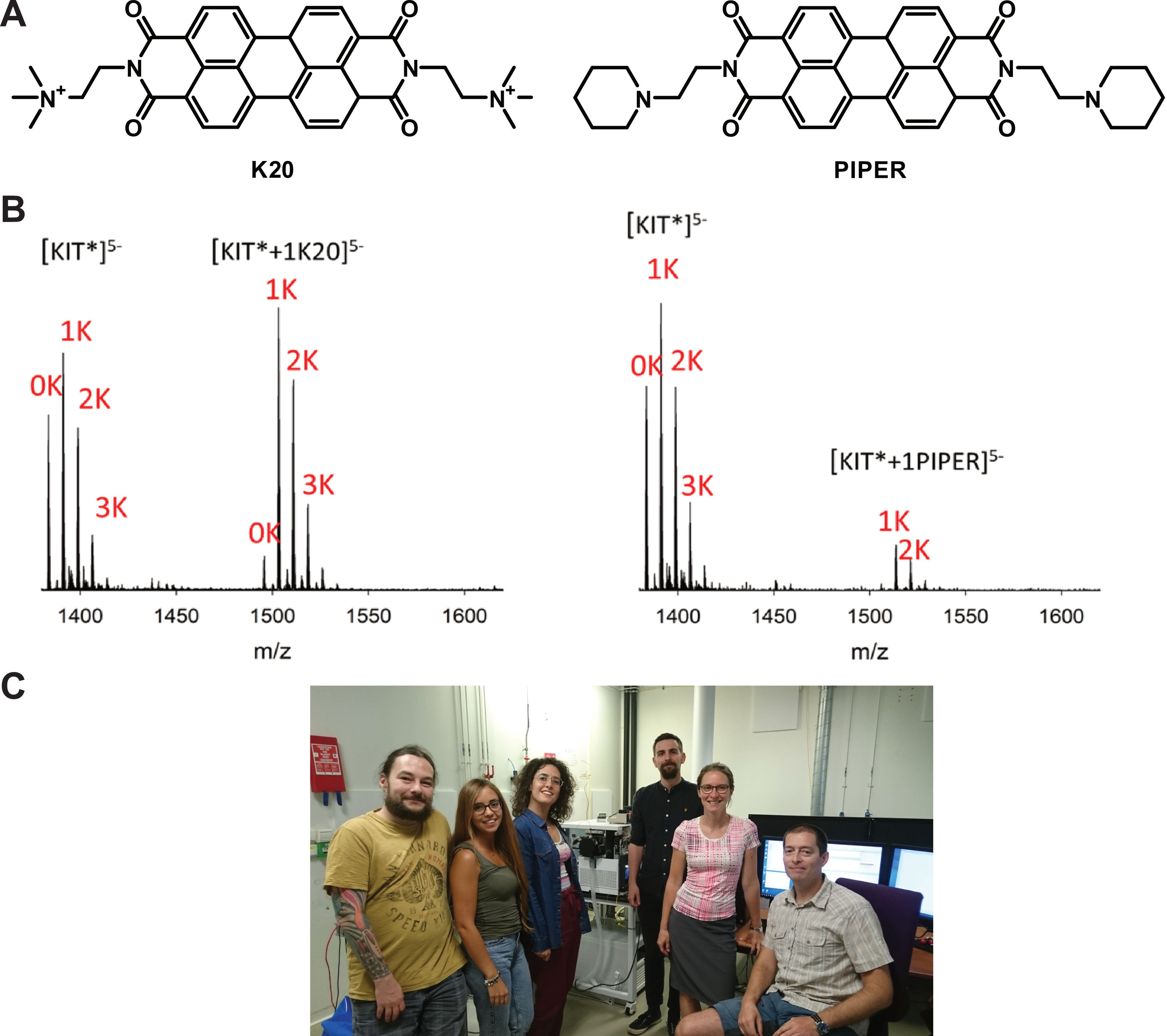
Nous avons montré par MS native [41] :

1. que le dérivé de pérylène K20 (Figure 5.20A) sélectionne cette topologie,

2. qu’un seul ion K⁺ est spécifiquement coordonné dans la structure (Figure 5.20B), qui est donc vraisemblablement composée de seulement deux quartets de guanines, et

3. que le ligand apparenté PIPER, dont seules les chaînes latérales diffèrent de K20 (Figure 5.20A), ne montre pas la même sélection conformationnelle. Cette dernière est donc un processus dépendant strictement de la composition des chaînes latérales du pérylène.

Ce projet a nécessité l’utilisation de relativement hautes concentrations de potassium pour que KIT* se structure (Figure 5.20B), ce qui a présenté un challenge technique intéressant.

5.3.2 Ligands avec des activités anticancéreuses ou antiparasitaires

Dans le cadre de collaboration avec le Pr. Jean Guillon (ARNA, UFR de pharmacie, Bordeaux ; Figure 5.21A), j’ai participé à la caractérisation de l’interaction de petites molécules à visée anticancéreuse ou antiparasitaire avec des G4s, par spectrométrie de masse native et dichroïsme circulaire.

J’ai caractérisé avec Matthieu Ranz une série de dérivés 2,9-bis[4-(pyridinylalkylaminométhyl)phényl]-1,10-phénanthroline ayant des propriétés antiprolifératives contre des lignées cellulaires de leucémie myéloïde humaine [42].

42. Guillon, J., Denevault-Sabourin, C., Chevret, E., Brachet-Botineau, M., Milano, V., Guédin-Beaurepaire, A., Moreau, S., Ronga, L., Savrimoutou, S., Rubio, S., Ferrer, J., Lamarche, J., Mergny, J.-L., Viaud-Massuard, M.-C., Ranz, M., Largy, E., Gabelica, V., Rosu, F., Gouilleux, F., et al. Design, synthesis, and antiproliferative effect of 2,9-bis[4-(pyridinylalkylaminomethyl)phenyl]-1,10-phenanthroline derivatives on human leukemic cells by targeting G-quadruplex. Archiv der Pharmazie, 2021, 354.

43. Guillon, J., Cohen, A., Boudot, C., Monic, S., Savrimoutou, S., Moreau, S., Albenque-Rubio, S., Lafon-Schmaltz, C., Dassonville-Klimpt, A., Mergny, J.-L., Ronga, L., Bernabeu de Maria, M., Lamarche, J., Lago, C.D., Largy, E., Gabelica, V., Moukha, S., Dozolme, P., Agnamey, P., et al. Design, Synthesis, and Antiprotozoal Evaluation of New Promising 2,9-Bis[(substituted-aminomethyl)]-4,7-phenyl-1,10-phenanthroline Derivatives, a Potential Alternative Scaffold to Drug Efflux. Pathogens, 2022, 11, 1339.

Avec Cristina Dal Lago (Master en séjour Erasmus au laboratoire, Padoue, Italie), nous nous sommes penchés sur l’étude une série de dérivés 2,9-Bis[(aminométhyl)]-4,7-phényl-1,10-phénanthroline présentant une activité antiprotozoaire contre les parasites Trypanosoma cruzi et Leishmania infantum [43].

Dans les deux études, nous avons montré que certains de ces dérivés interagissent avec les G4s de façon modérée (\(K_d\) de l’ordre du micromolaire) sans établir de lien avec leur propriétés anticancéreuse ou antiparasitaire. J’ai également encadré Mathilde Melot et Antoine Quaresima (Master, pharmaciens, Bordeaux) sur cette thématique.

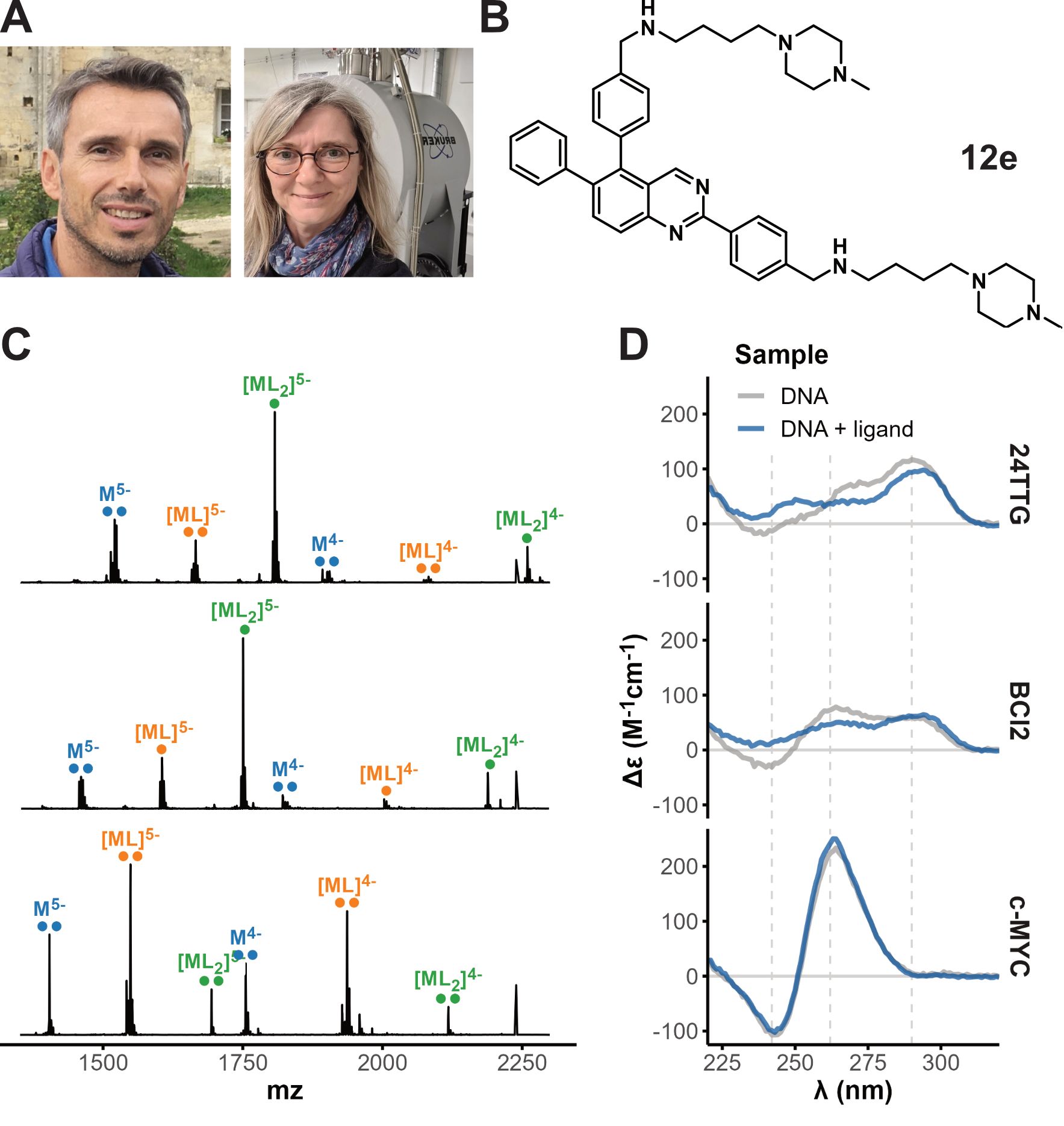
Plus récemment, avec Corinne Buré de la plateforme de spectrométrie de masse de l’IECB, nous avons étudié des dérivés de phénylquinazolines et phénylquinolines aux propriétés anticancéreuses [44]. Un dérivé m’ayant paru intéressant est 12e, qui se lie avec des affinités de l’ordre du micromolaire aux G4s des promoteurs BCl2 et c-MYC et de la séquence télomérique humaine (24TTG) (Figure 5.21). Dans le dernier cas, des complexes avec deux 12e se forment coopérativement (\(K_{d1} =\) 14, \(K_{d2} =\) 1.9 µM), en déplaçant l’équilibre conformationnel de 24TTG. L’éjection d’un cation ammonium détecté en masse (Figure 5.21C) et la signature CD (Figure 5.21D) suggèrent la formation d’un G4 antiparallèle à deux tétrades, ou l’intercalation d’un des deux ligands (ce qui est beaucoup moins probable). À l’inverse, les complexes 1:1 conservent leurs deux cations ammoniums, ce qui indique que ce premier complexe conserve la topologie originale du G4, mais que celle-ci est peu favorable à l’interaction.

44. Guillon, J., Le Borgne, M., Milano, V., Guédin-Beaurepaire, A., Moreau, S., Pinaud, N., Ronga, L., Savrimoutou, S., Albenque-Rubio, S., Marchivie, M., Kalout, H., Walker, C., Chevallier, L., Buré, C., Largy, E., Gabelica, V., Mergny, J.-L., Baylot, V., Ferrer, J., et al. New 2,4-bis[(substituted-aminomethyl)phenyl]phenylquinazoline and 2,4-bis[(substituted-aminomethyl)phenyl]phenylquinoline Derivatives: Synthesis and Biological Evaluation as Novel Anticancer Agents by Targeting G-Quadruplex. Pharmaceuticals, 2023, 17, 30.

Figure 5.21. A. Jean Guillon et Corinne Buré. B. Structure de 12e. C. Spectre de masse native de 24TTG, BCl2 et c-myc (de haut en bas), dans un pseudo-tampon acétate d’ammonium, en présence de deux équivalents de 12e (M = oligonucléotide monomérique, L = 12e). D. Spectres CD correspondants.

5.4 Développement de logiciels open source pour l’analyse de données

L’ensemble de mes contributions open-source sont déposées sur Github : github.com/EricLarG4.

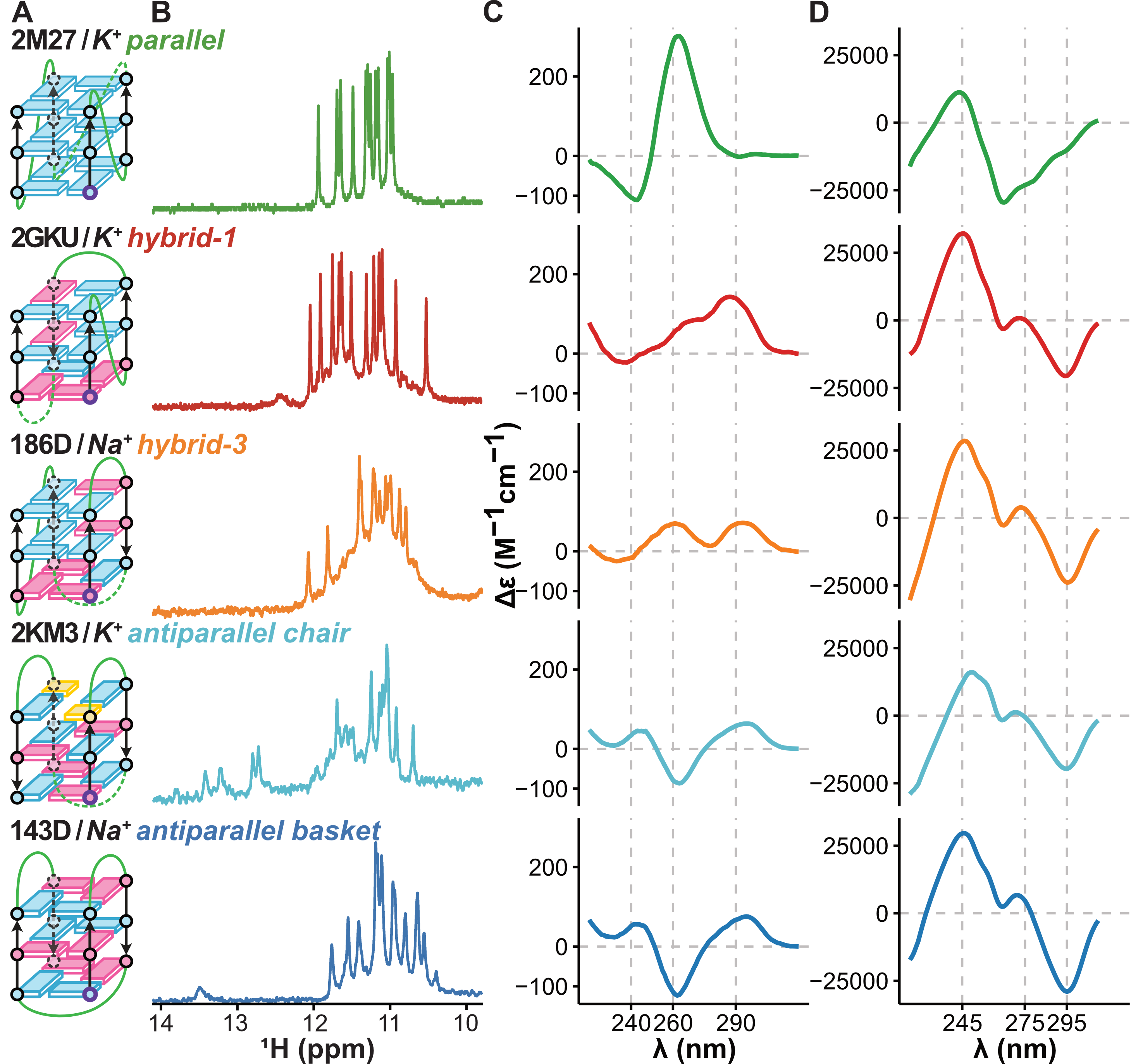
5.4.1 Détermination de topologies d’acides nucléiques G4 par spectroscopie UV-vis et dichroïsme circulaire

Dans le cadre d’une collaboration avec J.-L. Mergny (École Polytechnique) et Samir Amrane (ARNA, INSERM U1212 ; Figure 5.47), qui a acquis des données spectroscopiques (UV-vis et dichroïsme circulaire) avec Amani Kabbara (doctorante, thèse soutenue en 2022), j’ai développé le logiciel Eps2Fold pour déterminer la topologie de structures d’ADN G4 à relativement haut-débit, par analyse en composantes principales de CD et de spectres UV [45]. Initialement, ces derniers étaient exploités sous forme de signatures IDS (Isothermal Difference Spectra), qui sont obtenues par la soustraction de spectres d’oligonucléotides structurés en G4 (en présence d’un cation comme le potassium) et non-structurés correspondant (en absence du cation, donc). C’est une version isotherme d’une autre signature plus couramment utilisée pour détecter la formation d’un G4, ou le spectre “non structuré” est acquis à haute température d’où son nom : TDS, pour Thermal Difference Spectra [46].

45. Largy, E., Guédin, A., Kabbara, A., Mergny, J.-L. et Amrane, S. Eps2Fold: a rapid method to characterize G-quadruplex DNA structures using single absorbance spectra. Nucleic Acids Research, 2025, 53.

47. Kypr, J., Kejnovska, I., Renciuk, D. et Vorlickova, M. Circular dichroism and conformational polymorphism of DNA. Nucleic Acids Research, 2009, 37, 1713.

50. del Villar-Guerra, R., Gray, R.D. et Chaires, J.B. Characterization of Quadruplex DNA Structure by Circular Dichroism. Current Protocols in Nucleic Acid Chemistry, 2017, 68.

L’intérêt des spectres CD pour étudier la topologie d’acides nucléiques n’est plus à démontrer [47–50]. Celui de l’IDS, en revanche, est moins évident. Bien que calculé à partir de données pouvant paraître très sommaires, l’IDS contient des informations structurales plus intéressantes qu’il n’y parait et possède l’avantage, par rapport au TDS, d’être une technique isotherme. Par exemple, lors de mon postdoctorat dans l’équipe de J.-L. Mergny, j’avais déjà observé que les signatures IDS des conformères de 222T en présence de KCl et NaCl différaient, ce qui m’avait permis d’acquérir des cinétiques d’interconversion du second vers le premier avec de simples spectres UV [51]. Grâce au faible temps mort de cette approche, et au contrôle de la température qu’elle permet, j’avais accédé à l’énergie d’activation de cette interconversion en mesurant ces cinétiques UV à différentes températures.

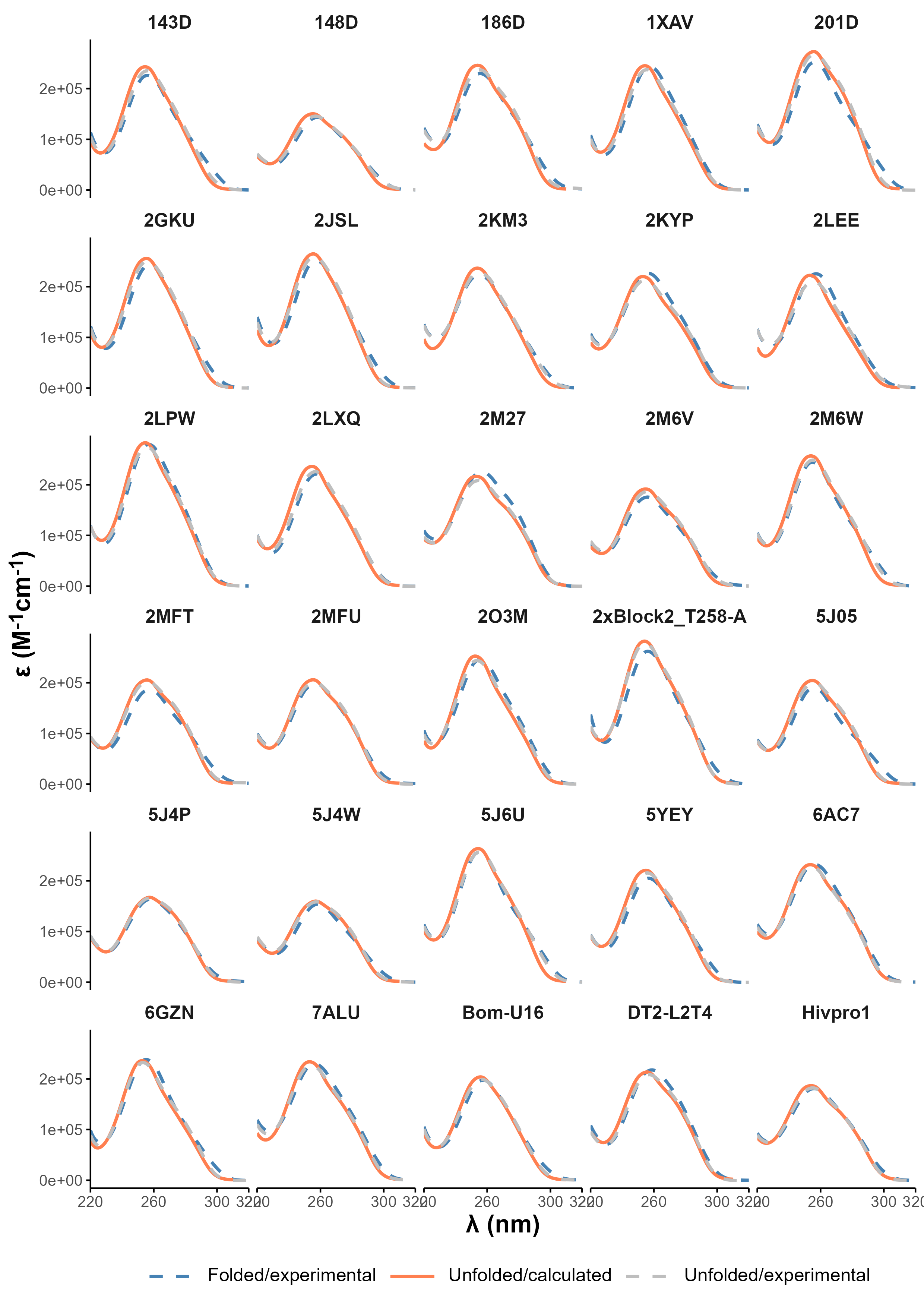
Il n’est cependant pas toujours aisé de déterminer la signature IDS d’un échantillon. Les G4s les plus stables (en particulier les parallèles à courtes boucles) peuvent se former en présences de faibles concentrations en cations et/ou sont difficiles à dessaler, du fait de leurs excellents \(K_d\) pour ces cations. En d’autres termes, le spectre UV acquis en absence de cations ne l’est pas vraiment, et la signature IDS qui en résulte est erronée. Pour référence, les séquences T95TT et T30177TT sont entièrement structurées à 5 µM en présence de quantités stœchiométriques de potassium [51]. Pour parer à ce problème, j’ai décidé de me passer de ce spectres difficile à acquérir expérimentalement, et de plutôt les calculer théoriquement. Pour cela, j’ai développé un algorithme permettant de calculer des spectres UV théoriques d’ADN non structuré, décrit dans la Section 5.5 (Figure 5.34). J’ai ensuite pu vérifier ce problème, et l’intérêt du calcul théorique de ces spectres, sur le set de données à ma disposition (Figure 5.22).

Figure 5.22. Comparaison des spectres UV “non structurés” calculés et expérimentaux (en absence de cation) et “structurés” (en présence de cation).

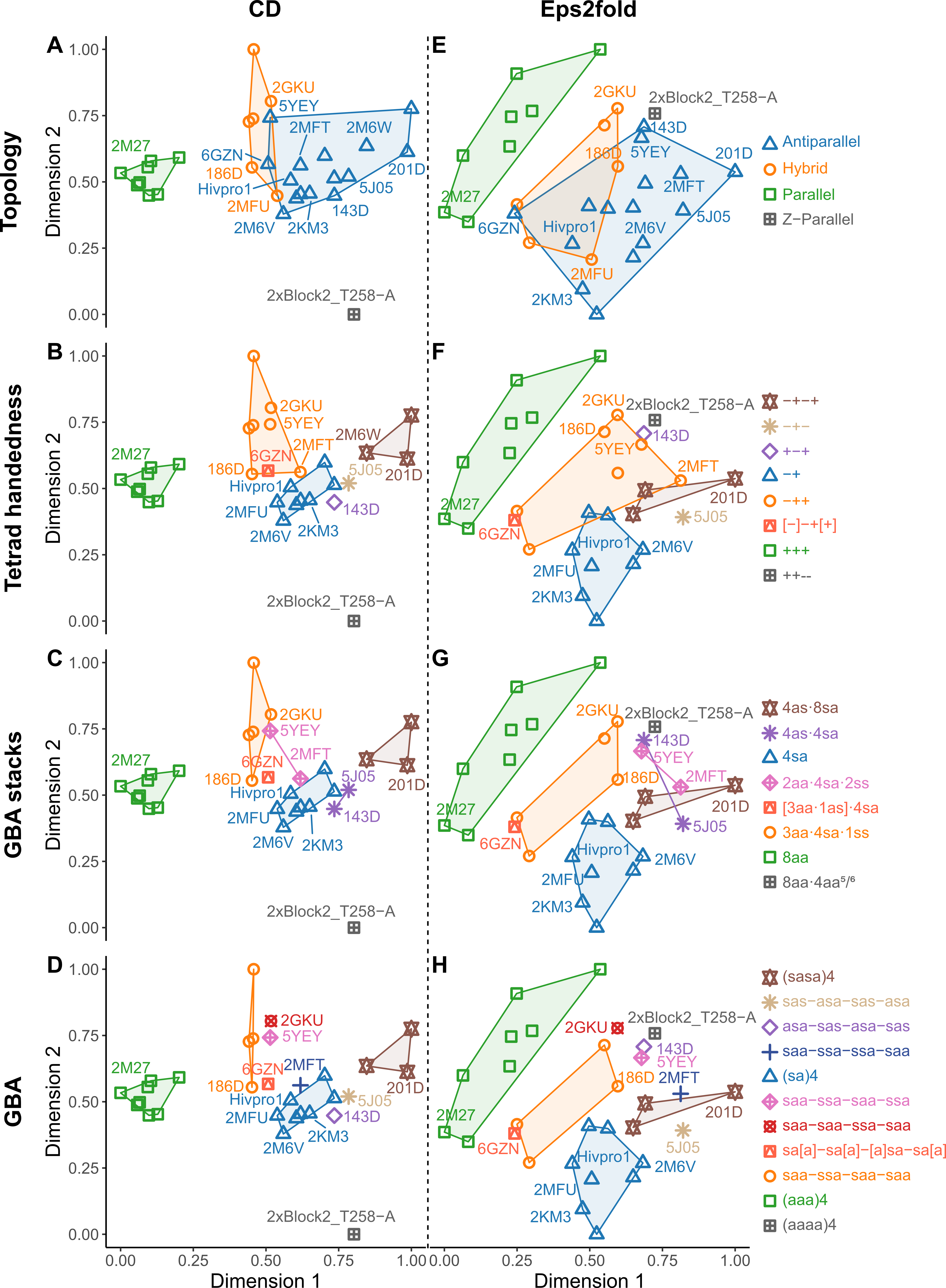
J’ai ensuite développé le programme Eps2Fold permettant le traitement des données UV et CD (import des données, soustraction de blancs, normalisation des données, calcul des signatures, analyse PCA, clustering), avec lequel nous avons construit une base de données spectrales pour laquelle la structuration des oligonucléotides a été validée, notamment par RMN (Figure 5.23).

Figure 5.23. Exemples de données spectroscopiques pour les conformères les plus classiques. A. Schéma des structures (bleu : anti, rose : syn, jaune : cytosines). B. Région imino de spectres de RMN ¹H. C. Spectres CD. D. Signatures Eps2Fold. C et D sont exprimés en \(\Delta\varepsilon\) (en M-1cm-1) mais sont des mesures différentes : C correspond au dichroïsme circulaire molaire \(\varepsilon_L - \varepsilon_R\) et D à une différence de coefficient d’extinctions molaires en fonction de la structure \(\varepsilon_{destructure} - \varepsilon_{structure}\).

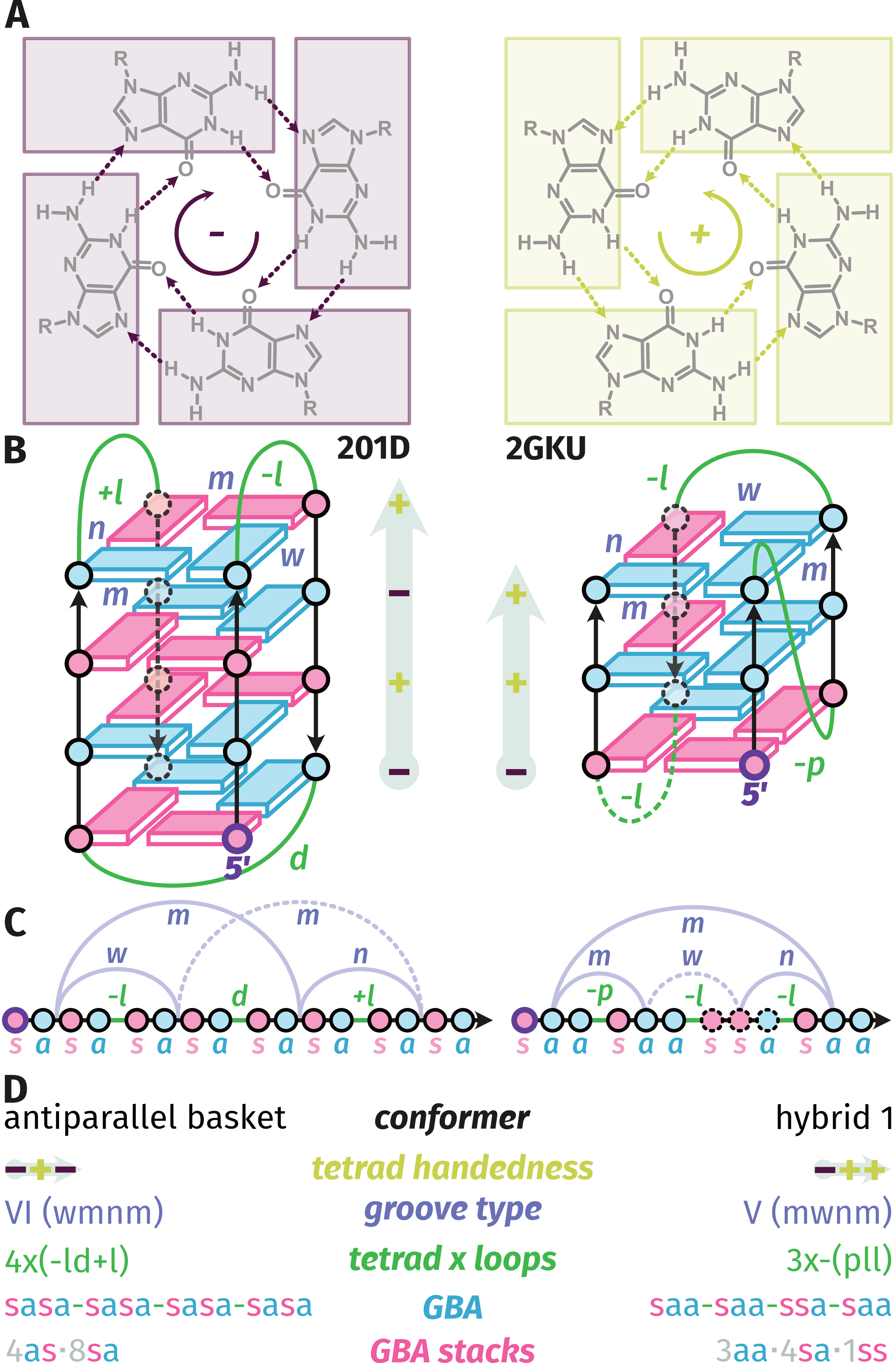
L’analyse en composantes principales et la détermination de clusters m’a amené à explorer les différents descripteurs structuraux des G4s : enchaînements d’angles glycosidiques des guanines (syn ou anti), de géométries de boucles, ou encore de sillons (Figure 5.24). En particulier, j’ai souhaité trouver un compromis entre la finesse de la description, sa capacité à décrire les différences observées expérimentalement, et sa lisibilité.

Figure 5.24. A. Sens de rotation (horaire (–) ou antihoraire (+)) des tétrades de guanines, définis par la direction des donneurs vers les accepteurs de liaisons H. B. Schémas des topologies antiparallèle basket (PDB : 143D [52]) et hybride 1 (PDB : 2GKU [53]). Les guanines bleues et roses présentent respectivement des angles de liaison glycosidique anti et syn. La chiralité des tétrades est notée + ou – selon la définition du panneau A, en les observant par le dessus et en commençant en 5’ (comme définit par V. Gabelica). Les boucles présentent des géométries propeller (p), latérale (l) ou diagonale (d), annotées avec + ou – lorsqu’elles relient les guanines dans un sens horaire ou antihoraire, respectivement, avec l’extrémité 5’ située en bas à droite de la structure (comme définit par M. Webba Da Silva [54]). Les sillons sont classés comme larges (w), moyens (m) ou étroits (n). C. Représentations linéaires des schémas du panneau B. D. Résumé des six descripteurs structuraux des topologies 143D et 2GKU du panneau B.

52. Wang, Y. et Patel, D.J. Solution structure of the human telomeric repeat d[AG3(T2AG3)3] G-tetraplex. Structure, 1993, 1, 263.

53. Luu, K.N., Phan, A.T., Kuryavyi, V., Lacroix, L. et Patel, D.J. Structure of the Human Telomere in K⁺Solution: An Intramolecular (3 + 1) G-Quadruplex Scaffold. Journal of the American Chemical Society, 2006, 128, 9963.

54. Dvorkin, S.A., Karsisiotis, A.I. et Webba da Silva, M. Encoding canonical DNA quadruplex structure. Science Advances, 2018, 4.

Ainsi, l’orientation syn/anti des liaisons glycosidiques (GBA) permet une séparation très fine des topologies mais est peu lisible (Figure 5.25D). À l’inverse, la séparation classique en topologies parallèle/antiparallèle/hybride est très peu performante, même en discriminant les antiparallèles chair et basket, mais très lisible (Figure 5.25A).

Figure 5.25. Comparaison des descripteurs structuraux : résultat de l’analyse en composantes principales des signatures CD et Eps2Fold du set de données expérimentales, où les données sont groupées par valeur du descripteur.

Au-delà du logiciel mise à disposition de la communauté, il est ressorti de cette étude que :

• Une combinaison donnée de géométries de stacking de guanines génère des signatures CD et Eps2Fold spécifiques, qui peuvent être résolues avec une granulométrie surprenante. Qualitativement, les tendances sont très similaires, et le CD intrinsèquement plus résolutif.

• Eps2Fold n’est pas un remplacement au CD, qui reste plus discriminant, mais peut venir en un complément encore plus rapide et facile à mettre en place. La technique pourrait être implémentée dans des expériences de criblage haut débit de G4s.

• L’interprétation des signatures Eps2Fold et CD ne doit pas se limiter à une inspection visuelle. Des changements structuraux discrets peuvent modifier ces signatures de façon modeste que seul un traitement des données systématique et sans biais humain peut détecter.

• Les descripteurs structuraux classiques pour décrire des résultats CD/Eps2Fold sont limités, en particulier quand ils se basent sur la polarité des brins (comme les topologies) plutôt que sur les géométries des guanines, puisque ce sont ces dernières qui expliquent le signal.

• Les descripteurs permettant des granulométries fines, comme l’enchaînement des GBA, permettent de discriminer efficacement les conformères G4s mais sont peu lisibles. Des descripteurs plus synthétiques, comme les chiralités de tétrades (Figure 5.25B) et les GBA stacks (Figure 5.25C, où l’on compte le nombre de stacks différents), présentent des compromis intéressant.

Dans la perspective de nos travaux futurs, nous visons à étendre cette approche à un éventail plus large de structures secondaires au-delà des G4s, et en explorant aussi les oligonucléotides d’ARN. En particulier, il sera essentiel d’évaluer la généralisabilité d’Eps2Fold en termes de résolution, ce qui pourrait nécessiter le développement de descripteurs structuraux adaptés à d’autres motifs de structures secondaires.

5.4.2 Analyse haut débit et haute précision d’UV-melting d’acides nucléiques

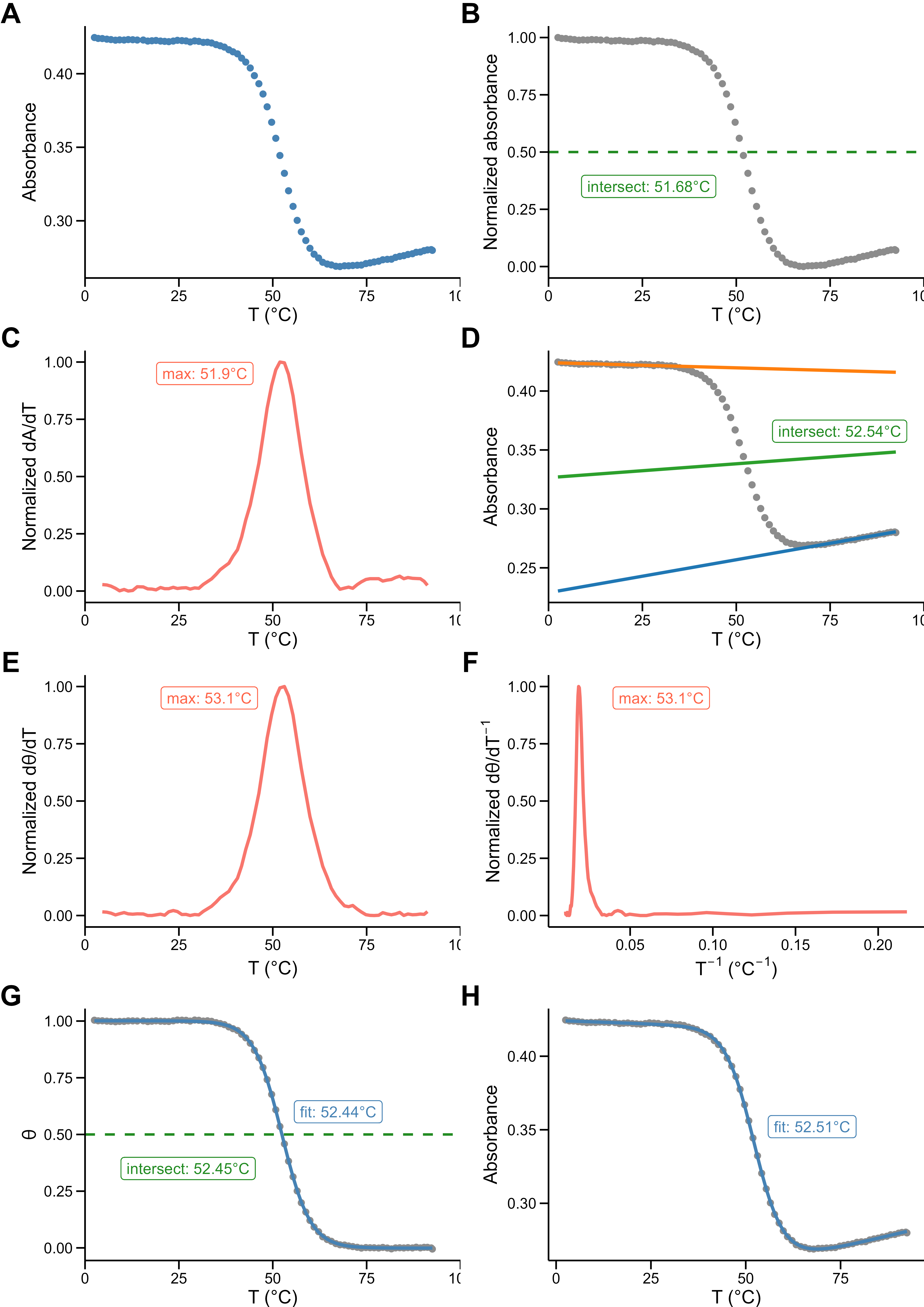
Les expériences de dénaturation thermique (melting), sont très couramment utilisées pour estimer la stabilité des structures secondaires d’acides nucléiques. Ces courbes sont le plus souvent obtenues avec une détection UV-vis, mais le CD et le FRET sont également fréquemment utilisés. Dans tous les cas, le signal est enregistré en fonction de la température et rend compte de l’état de repliement intramoléculaire et/ou d’association intermoléculaire des oligonucléotides (Figure 5.26A). Typiquement, la dénaturation de l’ADN duplex est suivie par l’hyperchromisme qui se produit à 260 nm. D’autres types de structures peuvent nécessiter des longueurs d’onde plus spécifiques, par exemple la dénaturation des G4s est caractérisée par une hypochromie à 295 nm [46].

46. Mergny, J.-L. Thermal difference spectra: a specific signature for nucleic acid structures. Nucleic Acids Research, 2005, 33, e138.

Dans la plupart des études, l’information quantitative extraite des courbes de dénaturation est la température de fusion (\(T_m\)), c’est-à-dire la température de dénaturation à mi-transition (Figure 5.26B–D). Elle peut être utilisée pour évaluer la stabilité des structures secondaires formées en solution. Elle permet de classer la stabilité thermique relative de différentes séquences ou d’une seule séquence dans différentes conditions (pH, force ionique, nature et concentration des cations). Le \(T_m\) est également très utilisé comme proxy de l’affinité de complexes d’oligonucléotides avec des ligands, en comparant les valeurs en présence et absence de ligands. Il ne s’agit pas d’une méthode de mesure directe et isotherme de l’affinité, mais c’est un moyen simple et populaire de classer les ligands.

Figure 5.26. Méthode de traitement des données de dénaturation thermique, illustrées avec les données brutes du panneau A (22GT, courbe de refroidissement). B. Intersection de \(A_{norm}=\) 0.5 (vert) avec la courbe d’absorbance normalisée à [0;1]. C. Maximum de la dérivée première \(dA/dT\). D. Intersection de la médiane (vert) des lignes de bases avec la courbe d’absorbance brute (lignes de base à basse température en orange et à haute température en bleu obtenues par régression linéaire). E. Maximum de la dérivée première de la fraction structurée par la température \(d\theta /dT\). F. Comme E mais par l’inverse de la température \(d\theta /dT^{-1}\). G. Intersection à 0.5 de la fraction structurée \(\theta\). H. Régression non-linéaire des données brutes avec un modèle thermodynamique.

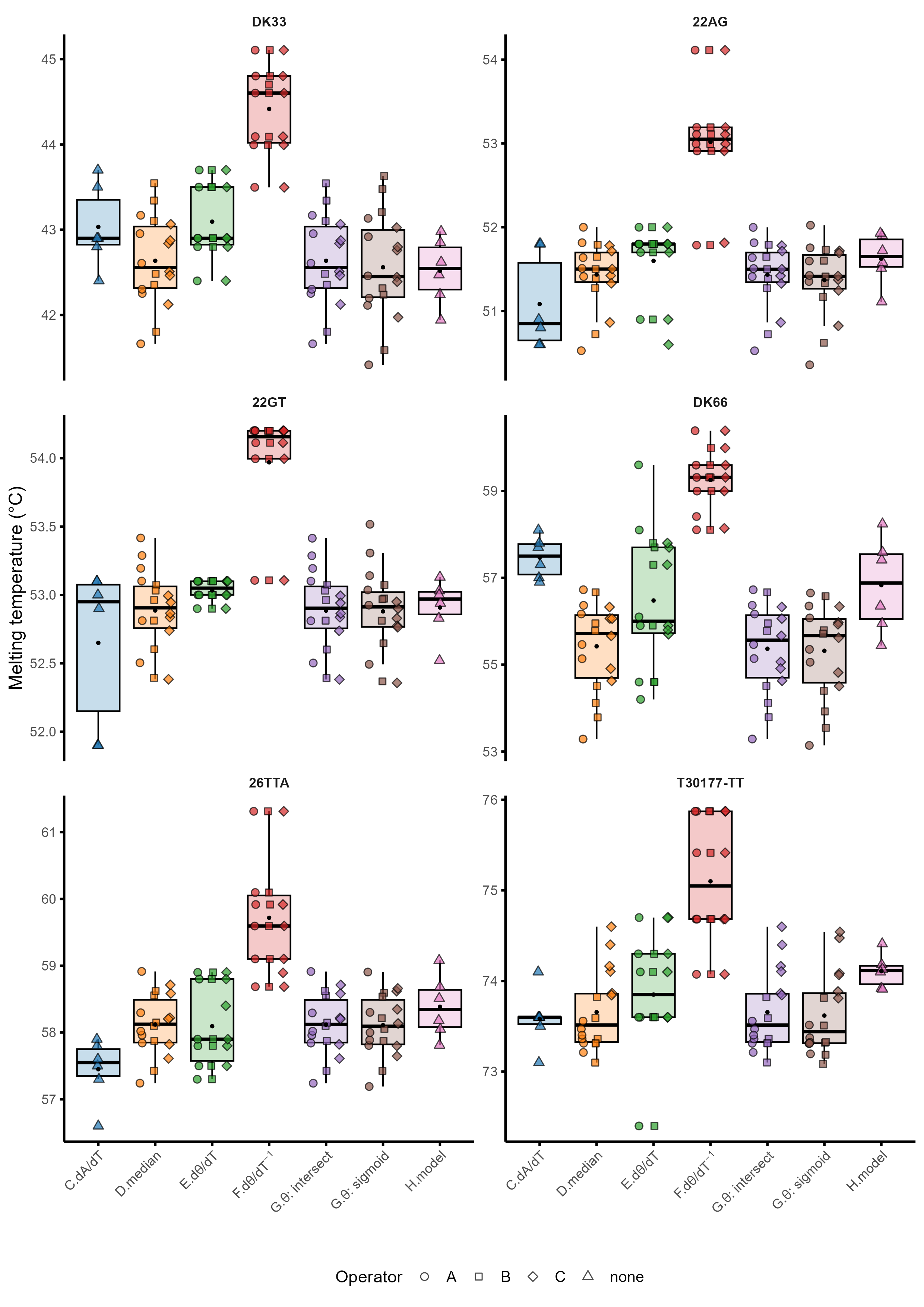
En réalité, ces courbes peuvent fournir plus que les seuls \(T_m\). Dans de nombreux cas, il est plus pertinent de déterminer la fraction structurée/associée \(\theta\) à la température d’intérêt de l’étude (Figure 5.26E–G). Il est par exemple possible pour deux oligonucléotides de \(T_m\) similaires d’avoir un \(\theta\) différent à la température d’étude, et l’utilisation de la \(T_m\) peut donc s’avérer simpliste voire erronée. Cependant, la détermination correcte de \(T_m\) nécessite de traiter les données afin de déconvoluer les contribution des la lignes de base non planes (pré et post-transition), qui résultent de la dépendance à la température des coefficients d’absorbtion molaires [55]. Ce traitement de données souffre de sa lenteur et de biais humains réduisant la précision des résultats, notamment le choix des régions pour la modélisation des lignes de bases. Plus généralement, l’utilisation de différentes méthodes de détermination de la \(T_m\) mène à une variabilité importante des résultats (\(\Delta T_m\) de 1.4°C dans l’exemple de la Figure 5.26). Il est fréquent de voir dans la littérature des valeurs de \(T_m\) avec un nombre de chiffres significatifs qui ne sauraient être compatibles avec la précision expérimentale.

55. Mergny, J.-L. et Lacroix, L. Analysis of Thermal Melting Curves. Oligonucleotides, 2003, 13, 515.

Figure 5.27. Comparaison de la précision des méthodes de détermination de la \(T_m\) sur 6 réplicats. Ici, les données de 6 oligonucléotides ont été traitées par 8 méthodes et 3 opérateurs différents.

Dans le cadre de l’établissement d’une base de données de G4s (voir Section 5.5, ci-après), j’ai été amené à devoir traiter un grand nombre de meltings pour lesquels je souhaitais avoir une approche la plus standardisée possible. La période de confinement consécutive à la pandémie de COVID a été propice au développement d’un algorithme permettant un traitement rapide et semi-automatisé de ces données. Cette approche a été intégrée à un logiciel nous ayant permis de construire la base de données [56]. Devant l’intérêt de certains collègues pour ces fonctionnalités, j’ai finalement décidé de développer un logiciel dédié, et open-source, meltR.

En plus des méthodes usuelles, une approche basée sur la modélisation thermodynamique non biaisée des données a été développée (Figure 5.26H), et comparée aux autre méthodes (Figure 5.27).

Le modèle repose sur l’expression des coefficients d’extinction \(\varepsilon_T\) comme la somme des contributions des formes structurées (folded, F) et non-structurées (unfolded, U), pondérées par leurs abondances relatives (Équation 5.1).

\[\varepsilon_T=\varepsilon_T^F \times \theta _T + \varepsilon_T^U \times (1-\theta _T) \tag{5.1}\]

La fraction foldée est définie par \(\theta = \frac{[F]}{[F]+[U]}\). En considérant un modèle simple à deux états \(F \Leftrightarrow U\) ayant une constante d’équilibre \(K\), \(\theta\) peut être exprimé par l’Équation 5.2, qui mène à l’Équation 5.3.

\[\theta = \frac{1}{1+K} \tag{5.2}\]

\[\varepsilon_T=\varepsilon_T^F \times \frac{1}{1+K} + \varepsilon_T^U \times \frac{K}{1+K} \tag{5.3}\]

\(\varepsilon_T^F\) et \(\varepsilon_T^U\) peuvent être modélisés comme des fonctions linéaires de la température (Équation 5.4), où \(a\) est la pente et \(b\) l’ordonnée à l’origine de ces lignes de base :

\[\varepsilon_T=(a^FT+b^F) \times \frac{1}{1+K} + (a^UT+b^U) \times \frac{K}{1+K} \tag{5.4}\]

\(K\) est exprimé dans l’Équation 5.5 par des quantités thermodynamiques d’intérêt.

\[-RTlnK = \Delta G^0 = \Delta H^0 - T\Delta S^0 \tag{5.5}\]

Les éventuels changement de capacité thermique dans la gamme de températures étudiée n’ont pas été pris en compte ici, car cela a mené à des sur-paramétrisations du modèle. À la température de melting, l’Équation 5.6 mène aux Équations 5.7 et 5.8.

\[ \Delta G_m^0 = \Delta H_m^0 - T\Delta S_m^0 = 0 \tag{5.6}\]

\[\Delta S_m^0 = \frac{\Delta H_m^0}{T_m} \tag{5.7}\]

\[\Delta G^0 = \Delta H^0_{m} (1- \frac{T}{T_m}) \tag{5.8}\]

Finalement, K peut être exprimé par \(exp(-\frac{\Delta H^0 (1- \frac{T}{T_m})}{RT})\) ce qui mène à l’Équation 5.9 :

\[A_T=(a^FT+b^F) \times \frac{1}{1+exp(-\frac{\Delta H^0 (1- \frac{T}{T_m})}{RT})} + (a^UT+b^U) \times \frac{exp(-\frac{\Delta H^0 (1- \frac{T}{T_m})}{RT})}{1+exp(-\frac{\Delta H^0 (1- \frac{T}{T_m})}{RT})} \tag{5.9}\]

meltR est disponible en ligne et permet de :

• Déterminer les températures de melting et paramètres thermodynamiques sans biais de l’opérateur,
• Déterminer les fractions structurées aux températures souhaitées,
• Analyser les courbes de chauffage et refroidissement indépendamment, afin de détecter d’éventuelles cinétiques lentes d’association/repliement,
• Automatiser toutes les étapes de l’analyse pour réduire les erreurs, accélérer et réduire la pénibilité du processus. Une dizaine d’échantillons peut être traitée en quelques secondes,
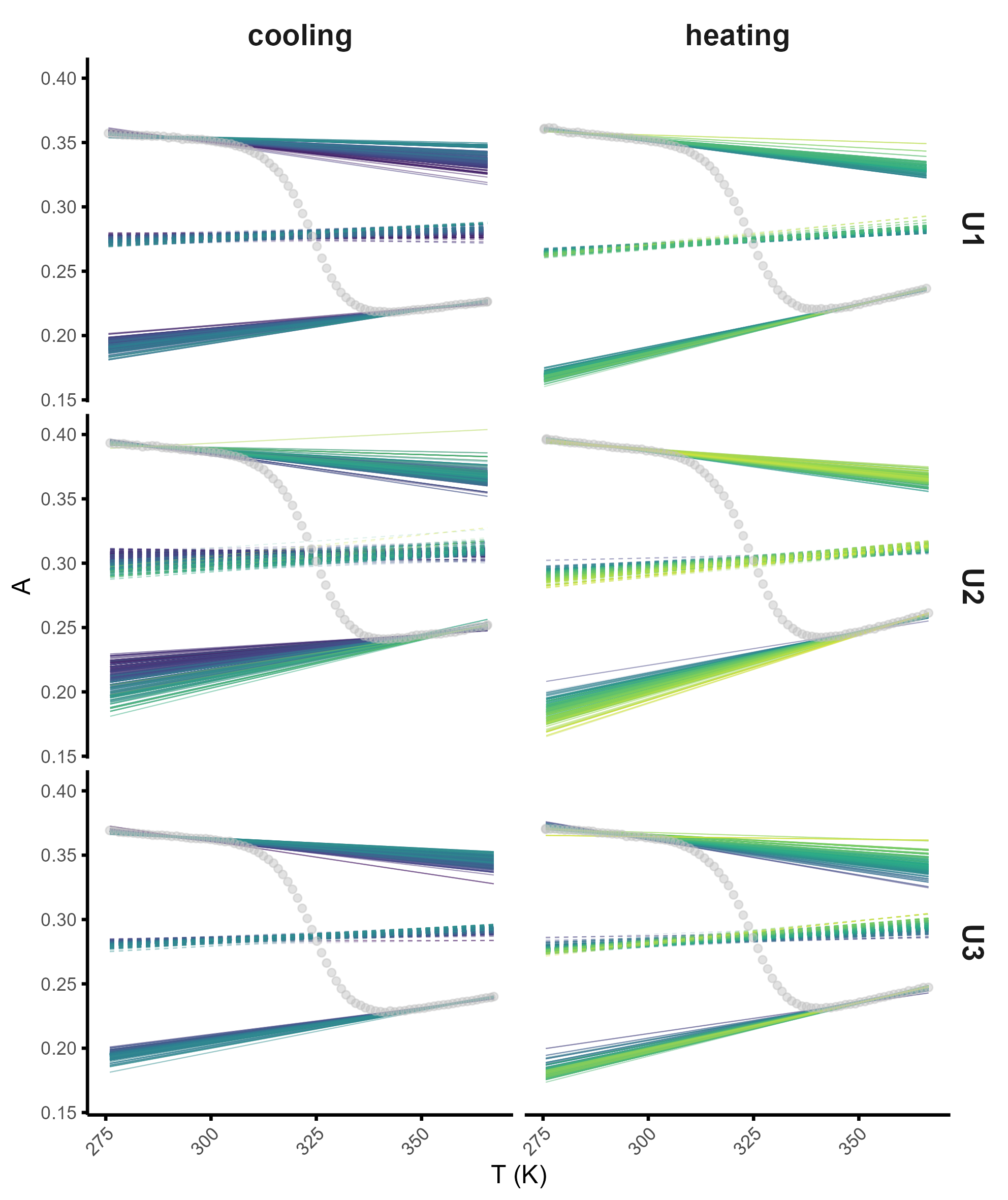
• Visualiser le résultat d’un traitement de données classique, par soustraction des lignes de base, en tenant compte de l’incertitude sur la détermination de ces lignes de bases. Plutôt que de considérer des régions discrètes et uniques pour chaque ligne de base, on entre plutôt des gammes possibles de régression. meltR permet ensuite de simuler un très grand nombre de lignes de bases dans ces régions, ce qui génère des distributions de \(T_m\) et \(\theta\). Cela permet d’illustrer visuellement les biais d’opérateur, ce qui a, a minima, une valeur ajoutée pédagogique. La Figure 5.28 montre les différences entre 1000 couples de lignes de bases pour trois réplicats de deux rampes de la dénaturation de 22AG, ce qui entraîne des différences significatives de \(T_m\) comme illustrées Figure 5.29.

Figure 5.28. Traitement de données d’UV-melting par la méthode tenant compte des lignes de bases, pour trois réplicats d’une expérience à deux rampes (refroidissement puis chauffe), sur l’oligonucléotide 22AG. 1000 couples de lignes de base ont été générés à partir d’un set d’autant de régions sur lesquelles les régressions linéaires ont été effectuées. L’intersection des médianes correspondantes (en pointillés) génère 1000 \(T_m\), illustrant la potentielle variabilité inter-opérateur.

Figure 5.29. Distribution des différences de \(T_m\) mesurées pour quatre oligonucléotides (groupés par réplicat et rampe) relatives à leur \(T_m\) moyenne. Ces différences augmentent généralement pour les espèces particulièrement stables ou instables, pour lesquelles la transition est proche des limites haute ou basse de la gamme de température explorée. Dans ces cas de figure, les régressions linéaires doivent être faites sur de petites régions, ce qui génère de l’erreur.

J’ai encadré plusieurs étudiants pour la génération de données expérimentales et le test du logiciel afin d’en estimer les performances : Matthieu Bonnardel (Licence, Bordeaux) : Axel Florent (DEUST, Bordeaux), et Matthieu Vida (Licence, Bordeaux).

L’unique perspective de ce projet est de le publier. S’il ne révolutionnera pas la biophysique des oligonucléotides, il constitue un outil pratique pour la communauté.

5.4.3 Spectrométrie de masse native d’acides nucléiques

Comme je l’ai brièvement exposé dans le chapitre Chapitre 4, l’HDX/MS est une méthode de plus en plus utilisée pour étudier la dynamique structurale et l’interaction des protéines, généralement avec une approche bottom-up ([Figure 4.4). Cette approche génère une grande quantité de données, dont le traitement est long et pénible.

Par conséquent, de nombreux logiciels ont été développés pour faciliter le traitement des données brutes HDX/MS (détection et identification des peptides, détermination de leur teneur en deutérium, modélisation et ajustement de la distribution isotopique) [57–67], le post-traitement (comparaison de la deutération entre les échantillons, évaluation de la signification statistique) et la visualisation [60, 63, 68–78].

57. Abzalimov, R.R. et Kaltashov, I.A. Extraction of local hydrogen exchange data from HDX CAD MS measurements by deconvolution of isotopic distributions of fragment ions. Journal of the American Society for Mass Spectrometry, 2006, 17, 1543.

67. Yamamoto, T., Yamagaki, T. et Satake, H. Development of Software for the In-Depth Analysis of Protein Dynamics as Determined by MALDI Mass Spectrometry-Based Hydrogen/Deuterium Exchange. Mass Spectrometry, 2020, 8, S0082.

60. Lou, X., Kirchner, M., Renard, B.Y., Köthe, U., Boppel, S., Graf, C., Lee, C.-T., Steen, J.A.J., Steen, H., Mayer, M.P. et Hamprecht, F.A. Deuteration distribution estimation with improved sequence coverage for HX/MS experiments. Bioinformatics, 2010, 26, 1535.

63. Lindner, R., Lou, X., Reinstein, J., Shoeman, R.L., Hamprecht, F.A. et Winkler, A. Hexicon 2: Automated Processing of Hydrogen-Deuterium Exchange Mass Spectrometry Data with Improved Deuteration Distribution Estimation. Journal of the American Society for Mass Spectrometry, 2014, 25, 1018.

68. Kan, Z., Ye, X., Skinner, J.J., Mayne, L. et Englander, S.W. ExMS2: An Integrated Solution for HydrogenDeuterium Exchange Mass Spectrometry Data Analysis. Analytical Chemistry, 2019, 91, 7474.

78. Janowska, M.K., Reiter, K., Magala, P., Guttman, M. et Klevit, R.E. HDXBoxeR: An R package for statistical analysis and visualization of multiple Hydrogen-Deuterium Exchange Mass-Spectrometry datasets of different protein states. Bioinformatics, 2024, 10.1093/bioinformatics/btae479.

Nous l’avons vu, j’ai lancé des travaux visant à démontrer que l’HDX/MS est également une excellente méthode pour étudier les structures secondaires d’acides nucléiques (Section 5.2.1) [2, 3]. Contrairement à l’approche standard utilisée pour les protéines, cette méthode ne nécessite pas d’étapes de quenching ou de dénaturation, ni de séparation chromatographique. Pour rappel, deux techniques ont été développées : i) mesure en temps réel de l’échange (RT-HDX), où chaque scan correspond à un moment précis de déutération et ii) mélange en flux continu (CF-HDX ; Figure 5.3C) où tous les scans MS d’une configuration donnée correspondent au même temps de déutération. Ces méthodes offrent plusieurs avantages : compatibilité avec des conditions natives, séparation de mélanges conformationnels par masse et structure, réduction du nombre d’analytes par injection tout en augmentant le nombre de points pour chaque cinétique (généralement une vingtaine contre, 4-5 en bottom-up). Cependant, ces approches présentent des défis spécifiques, notamment le besoin de calculer des enveloppes isotopiques théoriques pour les analytes d’ADN, dont les sites échangeables diffèrent de ceux des peptides. De plus, il est nécessaire de prendre en compte les interactions non covalentes avec des cations et des molécules organiques, qui peuvent d’ailleurs aussi contenir des sites échangeables.

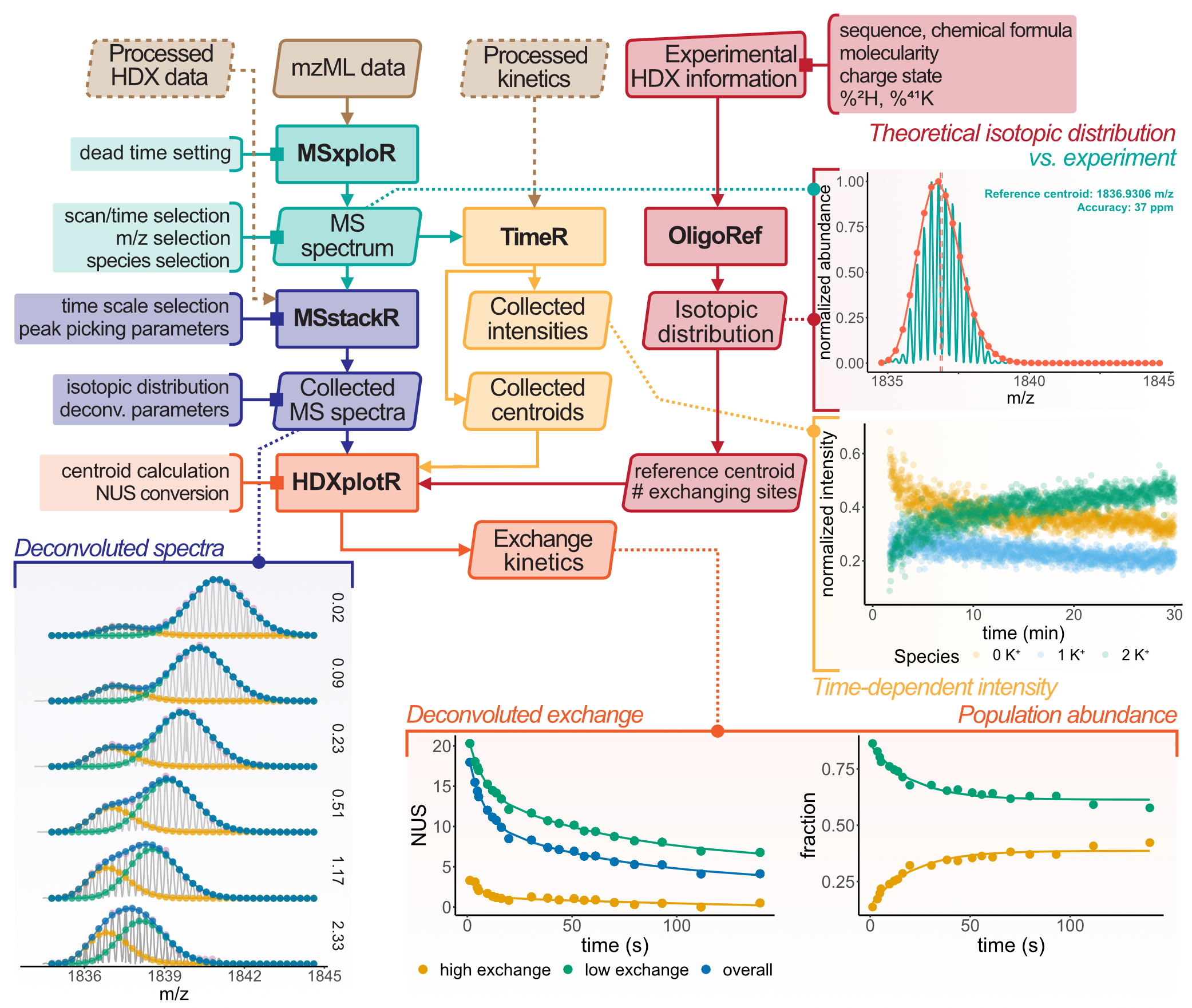
Pour répondre à ces exigences, j’ai développé une application open-source nommée OligoR [79]. Cette application, codée en R, est conçue pour traiter les données brutes de HDX/MS des oligonucléotides, allant de l’importation des données brutes de spectrométrie de masse à la génération de figures pour publication, en passant par la détermination des centroïdes et le calcul de la deutération (Figure 5.30).

OligoR permet également de déterminer le nombre de sites échangeable d’un oligonucléotide, le calcul de distributions isotopiques d’oligonucléotides et de leurs complexes directement à partir de leurs séquences et/ou formules brutes (Figure 5.31A, D), et la déconvolution des distributions bimodales (Figure 5.32), ce qui est crucial pour l’analyse des cinétiques d’échange et des constantes d’équilibre sous-jacentes que nous avons exploitées ci-avant (Section 5.2.1.2). Finalement, OligoR peut être utilisé pour l’automatisation du traitement de données de titrations et cinétiques de complexations en spectrométrie de masse native (Figure 5.31E, F).

Figure 5.30. Flux de travail dans OligoR avec les principaux paramètres et les visualisations de résultats. Les données en entrée sont représentées en marron ; les données en pointillés sont des données prétraitées exportées sous forme de fichier .xlsx lors d’une session précédente. Les données HDX traitées sont composées de deux fichiers (spectres MS sélectionnés et déconvolués). Les figures ont été générées avec OligoR à partir des données d’HDX/MS du G4 télomérique humain 23TAG et de la cinétique d’interaction du K⁺ avec ce même G4.

Figure 5.31. Exemples d’utilisation d’OligoR. À gauche : expérience CF-HDX d’un complexe 23TAG•PhenDC3 en présence de 23TAG libre, séparés en masse. A. Détermination empirique du centroïde de référence entièrement échangé (ligne bleue) et comparaison avec la théorie (ligne et points orange) pour le complexe 23TAG•PhenDC3 (C₂₆₄H₃₀₃O₁₄₁N₁₀₀P₂₂K₁, z = 4- avec 51 protons échangeables, 9%D). B. Spectres de masse collectés pour le 23TAG et le 23TAG•PhenDC3 pour différents points de temps de mélange. La sélection automatisée des pics est illustrée par des points roses. C. Cinétique d’échange apparente correspondante (points) et régression non linéaire avec l’Équation 5.12 (lignes). A droite : Expérience RT-HDX acquise pendant 90 minutes (temps mort : 40 s). D. Identique à A pour T30177-TT liant deux K⁺ (C₁₉₀H₂₃₀O₁₁₉N₇₄P₁₈K₂, z = 4- avec 43 protons échangeables, 9%D). E. Calculs des centroïdes pour chacun des 3867 scans. F. Cinétique d’échange apparente correspondante pour chaque scan (points) et régression non linéaire avec l’Équation 5.12 (lignes).

Au cœur de ce logiciel se trouvent des calculs simples, validés notamment par notre première publication sur le sujet [2]. Ainsi, le nombre de sites échangeables d’un oligonucléotide est donné par l’Équation 5.10.

\[ nX=3×n_{dG}+2×(n_{dA}+n_{dC})+n_{dT} \tag{5.10}\]

La convolution de la distribution en deutérons, qui suit la loi binomiale [2], et de la distribution isotopique naturelle, est implémentée en utilisant une transformation de Fourier rapide [80].

2. Largy, E. et Gabelica, V. Native Hydrogen/Deuterium Exchange Mass Spectrometry of Structured DNA Oligonucleotides. Analytical Chemistry, 2020, 92, 4402.

80. Sadygov, R.G. Poisson Model To Generate Isotope Distribution for Biomolecules. Journal of Proteome Research, 2017, 17, 751.

Les centroïdes au temps d’incubation \(t\), calculées comme la moyenne des \(m/z\) pondérée par leurs intensités, sont converties en nombre de sites non-échangés \(NUS\) en tenant compte du centroïde de l’oligonucléotide entièrement échangé \(m/z_{\infty}\), de l’état de charge \(z\), des proportions de deutérium en solution avant (\(DC_0\)) et après (\(DC_\infty\)) et des masses atomiques des isotopes (Équation 5.11).

\[ NUS_t=\frac{(m/z_t-m/z_∞ )×|z|)}{(DC_0-DC_{\infty})(m_D-m_H)} \tag{5.11}\]

Les cinétiques d’échanges sont ensuite modélisées avec le nombre minimales de décroissances exponentielles (généralement une par ordre de grandeur de temps d’incubation), en utilisant l’Équation 5.12, où \(N_i\) et \(k_i\) sont le nombre de sites et la constante de vitesse de la décroissante \(i\).

\[ NUS_t=NUS_∞+∑_{i=1}^j(N_i×e^{-k_i×t}) \tag{5.12}\]

La déconvolution de distributions isotopiques est l’innovation la plus importante de ce travail. Plutôt que de se reposer sur l’utilisation de Gaussienne comme certains logiciels pour l’analyse de données HDX/MS de protéines, j’ai ici implémenté une optimisation tirant partie de la capacité d’OligoR à calculer des distributions isotopiques deutérées. L’algorithme minimise la différence d’intensité des pics \(I\) entre les distributions calculées (\(model\)) et expérimentales (\(exp\)) en modifiant la deutération de l’oligonucléotide (Équation 5.13).

\[ S=∑_i{\Delta I_{i=1}^2}=∑_i(I_{model(i)}-I_{exp(i)})^2 \tag{5.13}\]

Pour des distributions multimodales, l’optimisation est réalisée en ajustant la deutération des distributions calculées \(j\) à partir desquelles une seule intensité totale pour chaque pic est calculée (Équation 5.14).

\[ I_{bimodal(i,j)} =∑_{(j=1)}^n(I_{model(i,j)}\times ab_j) \tag{5.14}\]

La beauté de cette approche est que seule des distributions physiquement possibles peuvent être générées, car les calculs sont bornés par les quantités de deutérium expérimentales et dépendent directement de la séquence de l’analyte. Seuls des résultats réalistes peuvent donc être obtenus. En outre, comme la largeur des distributions est fixe pour une séquence et une deutération donnée, ce que reflète parfaitement OligoR, il est possible de détecter des distributions “cachées”, c’est à dire deux distributions partiellement superposées qui apparaissent comme unique (voir les panneaux du bas de la Figure 5.32).

À l’inverse, dans les cas où une seule population est suffisante, les distributions bimodales vont tout de même donner de meilleurs résultats (entendre un \(RSS\) plus faible) en raison du plus grand nombre de paramètres. Cela générerait des faux positifs. Pour parer à cela, OligoR identifie automatiquement le modèle statistiquement meilleur par le calcul de la valeur \(p\) de la statistique \(F\),² définie dans l’Équation 5.15, où \(df\) est le degré de liberté et \(mono\) et \(bi\) se réfèrent aux modèles mono- et bimodaux, respectivement (Figure 5.32).

² L’hypothèse nulle est que le modèle bimodal n’explique pas mieux la variance que le modèle monomodal

\[ F=\frac{\frac{RSS_{mono}-RSS_{bi}}{RSS_{bi}}}{\frac{df_{mono}-df_{bi}}{df_{bi}}} \tag{5.15}\]

Le développement du logiciel est pour le moment stoppé puisqu’il est fonctionnel et répond pleinement à nos besoins. Dans un futur proche, il sera nécessaire d’intégrer le traitement de données HDX-MS/MS pour assurer l’identification des fragments, la modélisation de leurs distributions isotopiques théoriques, la détermination de leur deutération en fonction du temps, et l’exploitation des cinétiques qui en résultent.

Figure 5.32. Exemple de modélisation de distributions isotopiques avec OligoR sur des distributions monomodales et bimodales, pour trois oligonucléotides (z = 4 , K⁺ = 2) et six temps d’incubation (en secondes, au-dessus des panneaux). Les données expérimentales sont en gris (peak picking en bleu), le fit global en orange, et les populations individuelles en vert et violet. Les lignes verticales en pointillés indiquent la position de leurs centroïdes respectifs. Dans le cas de 23TAG, l’abondance de la population isotopique fortement échangée augmente, ce qui suggère la présence d’une cinétique EX1 [3, 62, 79, 81]. Au contraire, il n’y a pas de changement dans les abondances des populations isotopiques du VEGF, de sorte que la distribution bimodale résulte probablement de conformations distinctes en solution.

3. Largy, E., Ranz, M. et Gabelica, V. A General Framework to Interpret HydrogenDeuterium Exchange Native Mass Spectrometry of G-Quadruplex DNA. Journal of the American Chemical Society, 2023, 145, 26843.

62. Guttman, M., Weis, D.D., Engen, J.R. et Lee, K.K. Analysis of Overlapped and Noisy Hydrogen/Deuterium Exchange Mass Spectra. Journal of the American Society for Mass Spectrometry, 2013, 24, 1906.

79. Largy, E. et Ranz, M. OligoR: A Native HDX/MS Data Processing Application Dedicated to Oligonucleotides. Analytical Chemistry, 2023, 95, 9615.

81. Weis, D.D., Wales, T.E., Engen, J.R., Hotchko, M. et Ten Eyck, L.F. Identification and characterization of EX1 kinetics in H/D exchange mass spectrometry by peak width analysis. Journal of the American Society for Mass Spectrometry, 2006, 17, 1498.

5.5 Base de données d’acides nucléiques G-quadruplexes

Les séquences d’ADN riches en guanine peuvent former des G4s [82–89], et ces G4s ont une fâcheuse tendance à adopter une variété de conformations en équilibre dynamique [1, 90–93]. Cet équilibre est fragile. En particulier, il peut être facilement déplacé en changeant la nature et la concentration en sels [51]. Le lecteur ayant fait l’effort d’atteindre cette page du manuscrit est certainement convaincu de tout cela.

82. Labudová, D., Hon, J. et Lexa, M. pqsfinder web: G-quadruplex prediction using optimized pqsfinder algorithm. Bioinformatics, 2019, 36, 2584.

89. Wong, H.M., Stegle, O., Rodgers, S. et Huppert, J.L. A Toolbox for Predicting G-Quadruplex Formation and Stability. Journal of Nucleic Acids, 2010, 2010.

90. Neidle, S. Beyond the double helix: DNA structural diversity and the PDB. Journal of Biological Chemistry, 2021, 296, 100553.

93. Marchand, A. et Gabelica, V. Folding and misfolding pathways of G-quadruplex DNA. Nucleic Acids Research, 2016, 44, 10999.

51. Largy, E., Marchand, A., Amrane, S., Gabelica, V. et Mergny, J.-L. Quadruplex Turncoats: Cation-Dependent Folding and Stability of Quadruplex-DNA Double Switches. Journal of the American Chemical Society, 2016, 138, 2780.

94. Marchand, A. et Gabelica, V. Native Electrospray Mass Spectrometry of DNA G-Quadruplexes in Potassium Solution. Journal of the American Society for Mass Spectrometry, 2014, 25, 1146.

41. Ceschi, S., Largy, E., Gabelica, V. et Sissi, C. A two-quartet G-quadruplex topology of human KIT2 is conformationally selected by a perylene derivative. Biochimie, 2020, 179, 77.

Ce qui n’a pas vraiment été évoqué, et ce n’est pas un point de détail pour l’analyste, c’est que la forte dépendance de ces équilibres conformationnels aux conditions expérimentales rend difficile la comparaison de résultats obtenus avec différentes techniques analytiques. Dans le cas particulier de la spectrométrie de masse native, dont il est beaucoup question ici, l’utilisation de KCl, non volatil, est limité à des concentrations beaucoup plus faibles qu’en conditions physiologiques. La concentration de référence pour les études de l’équipe de V. Gabelica est de 1 mM KCl, dans un tampon TMAA (100 mM) [94], même si nous avons occasionnellement infusé des solutions plus salées mais toujours de l’ordre du millimolaire (Section 5.3.1.2) [41]. Ces concentrations sont deux ordres de grandeur inférieures à celles utilisées dans nombre de méthodes classiques pour étudier les structures et interactions de G4s (UV/Fluorescence/CD/FRET(-melting), RMN, SPR, ITC et bien d’autres), qui reflètent mieux les conditions physiologiques. Cela est problématique pour l’interprétation structurale des résultats de masse native, pour laquelle on est en droit de se demander si les conformères formés sont les mêmes que ceux déposés dans la PDB.

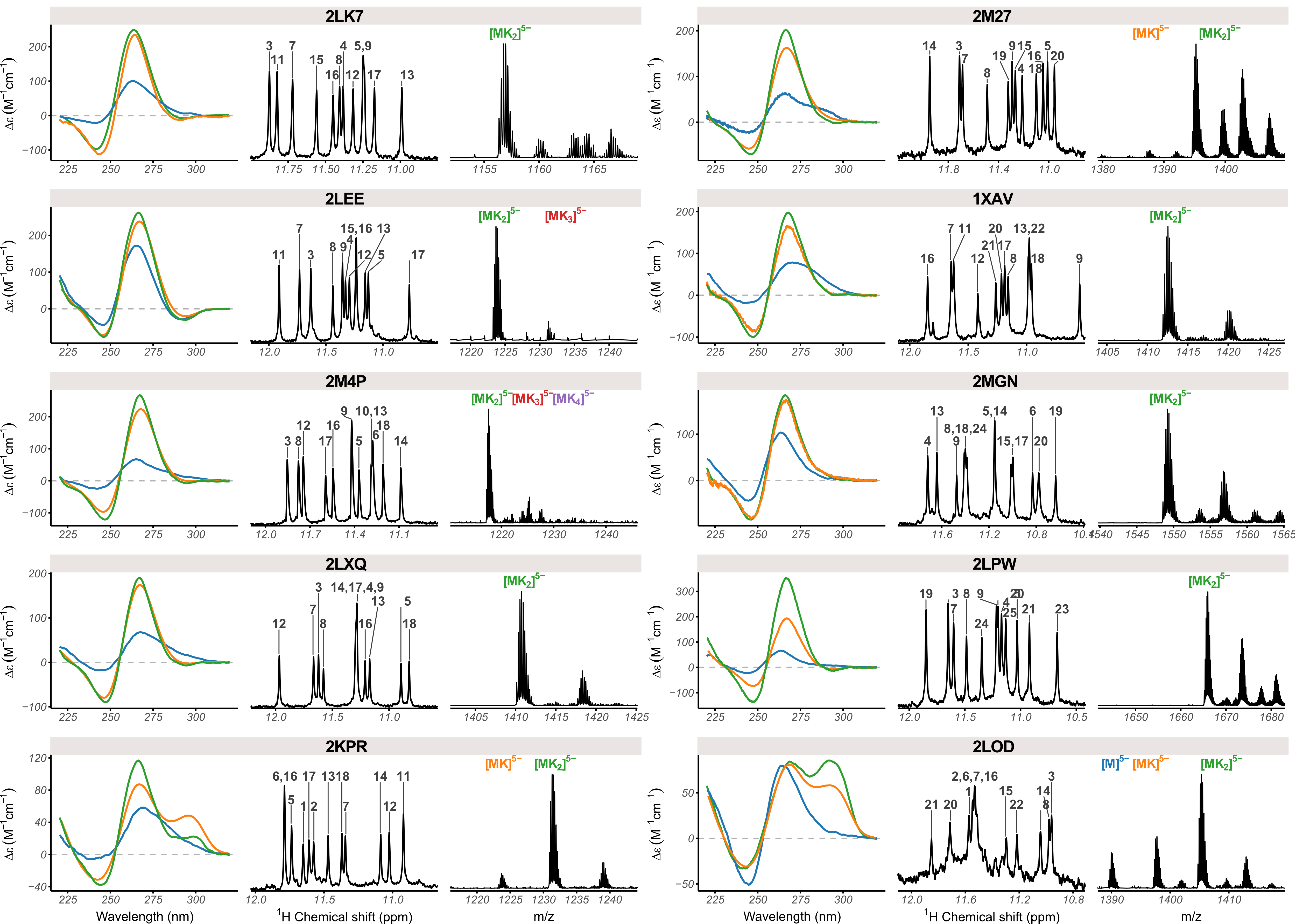
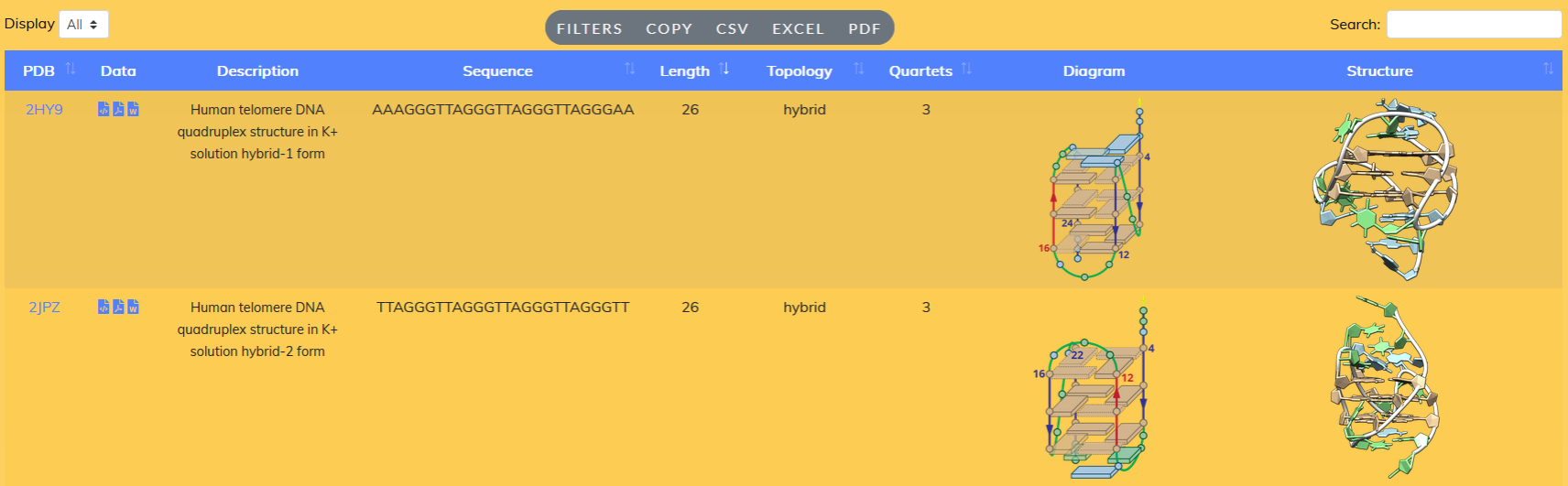
Nous avons donc souhaité établir une base de données de séquences formant des G4s, pour lesquelles il est établi que leurs structures dans le tampon “Native MS” (100 mM TMAA + 1 mM KCl) correspond à celles de référence, c’est à dire résolues par RMN et déposée dans la PDB [95]. Pour cela, Anirban Ghosh, un postdoctorant de l’équipe (désormais Senior Staff Scientist au CEITEC, République Tchèque), à fait l’acquisition des spectres de spectrométrie de masse native, de RMN du proton, de spectroscopie CD, et les courbes de dénaturation thermiques (par UV) en conditions Native MS et de référence (dépendantes des conditions expérimentales reportées dans la PDB). Le but a ensuite été de sélectionner les séquences ayant des spectres RMN et CD similaires dans ces deux conditions (Figure 5.33), puis de publier une base de données comprenant l’ensemble de ces données expérimentales.

95. Ghosh, A., Largy, E. et Gabelica, V. DNA G-quadruplexes for native mass spectrometry in potassium: a database of validated structures in electrospray-compatible conditions. Nucleic Acids Research, 2021, 49, 2333.

Figure 5.33. Exemples de spectres CD, RMN et de masse native pour dix oligonucléotides de la base de données. Les courbes CD sont colorées par concentration en KCl (vert : ~ 100 mM, rouge : 1 mM, bleu : 0).

Mes services ont été requis pour le mettre en place un traitement des données automatisé, fournissant des figures normées, et pour la mise en place de la base de données en ligne. Des activités dont je me suis principalement acquittées pendant le confinement, et qui ont également été le point de départ de meltR (Section 5.4.2).

Pour le traitement de données, j’ai développé une interface Shiny en R intégrant plusieurs fonctionnalités :

• Filtre des données par nom de la séquence, séquence, topologie, tampon, sel

• Attribution des pics des spectres de masse (automatisée) et de ¹H-RMN (manuel)

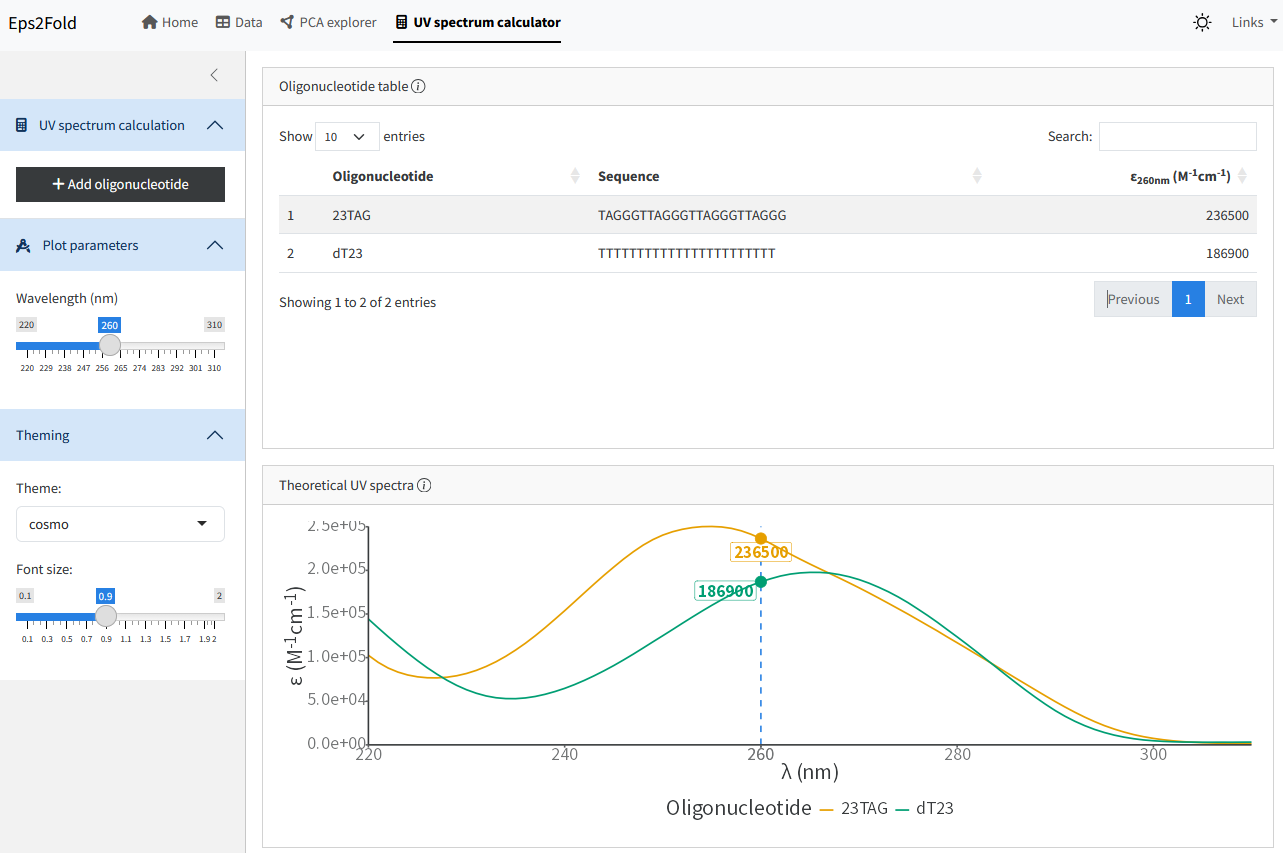
• Calcul des coefficients d’extinction molaire à 260 nm \(\varepsilon_{260 nm}\) des oligonucléotides, par la méthode de Tataurov et al. [96], c’est à partir de leur séquence et de l’Équation 5.16, où \(\varepsilon_i\) est le coefficient du nucléotide \(i\), \(\varepsilon_{i, i+1}\) celui du doublet de nucléotide en position \(i; i+1\) et \(N_b\) le nombre total de nucléotides. C’est cet algorithme que j’ai ensuite utilisé pour le projet Eps2Fold décrit en Section 5.4.1. Le logiciel associé dispose d’un onglet dédié pour le calcul des coefficients d’extinctions molaires (et de spectres d’absorbance) à partir de séquences oligonucléotidiques (Figure 5.34).

96. Tataurov, A.V., You, Y. et Owczarzy, R. Predicting ultraviolet spectrum of single stranded and double stranded deoxyribonucleic acids. Biophysical Chemistry, 2008, 133, 66.

\[ \varepsilon_{260 nm} = \sum_{i=1}^{N_b-1}\varepsilon_{i,i+1} - \sum_{i=2}^{N_b-1}\varepsilon_{i} \tag{5.16}\]

• Correction du blanc, des lignes de base, et conversion en ellipticités molaires \(\Delta\varepsilon\) (M^-1cm^-1) des données CD \(\theta\) (mdeg) avec l’Équation 5.17, où \(C\) et \(l\) sont la concentration molaire et la longueur du trajet optique, respectivement.

\[ \Delta \varepsilon = \frac{\theta}{32980 \times C \times l} \tag{5.17}\]

• Détermination des fractions structurées et des \(T_m\) à partir des courbes de dénaturation thermique, avec l’Équation 5.9. Il s’agit de l’embryon de ce qui deviendra meltR (Section 5.4.2).

• Réduction du bruit expérimental des spectres de masse

• Lecture/écriture de bases de données. La version finale est disponible sur Zenodo [56].

• Génération automatisée des figures et rapports disponibles en ligne.

56. Anirban Ghosh, Largy, E. et Gabelica, V. g4dbr: A database of validated DNA G-quadruplexes structures in native mass spectrometry conditions Zenodo (2020).

Figure 5.34. Copie d’écran du calculateur de spectres UV et coefficients d’extinction molaire intégré à Eps2Fold.

Au final, 28 séquences ont été retenues. La base de données g4dbr est disponible en ligne (Figure 5.35) et est utilisée, a minima par les membres de l’équipe. Plus de 7000 utilisateurs uniques se sont connectés du monde entier depuis sa mise en ligne.³ Surtout, elle nous a permis de plus facilement et rapidement rationaliser nos travaux en termes de structure. Un exemple récent d’utilisation de cette base de données est présenté en Section 5.3.1.1.

³ Top 10 : Chine, USA, France, Japon, Italie, Inde, Singapour, Royaume-Uni, Allemagne, République Tchèque. Il est intéressant de voir que l’on retrouve des pays avec de petites populations mais actives dans la communauté G4.

Figure 5.35. Copie d’écran de g4dbr (https://ericlarg4.github.io/G4_database.html)

5.6 Mécanique quantique et moléculaire de biomolécules

5.6.1 Contexte

La thématique la plus récente que j’ai abordée, et la première initiée dans l’équipe PRISM, est l’implémentation de calculs de dynamiques moléculaires (MD) de structures d’acides nucléiques non canoniques, avec deux objectifs. Le premier, celui qui a amené l’énergie d’activation nécessaire à l’initiation de ce travail, est l’utilisation de dynamiques moléculaires contraintes (rMD), par les données RMN, comme dernière étape dans la résolution de structures d’acides nucléiques par RMN, avant dépôt sur la PDB. Le second objectif est l’utilisation de MD pour mieux comprendre, ou anticiper, des résultats expérimentaux. En particulier, je présente dans ce document des applications sur des complexes G4/petites molécules (Sections 5.3.1.1, ci-avant, et 5.6.4).

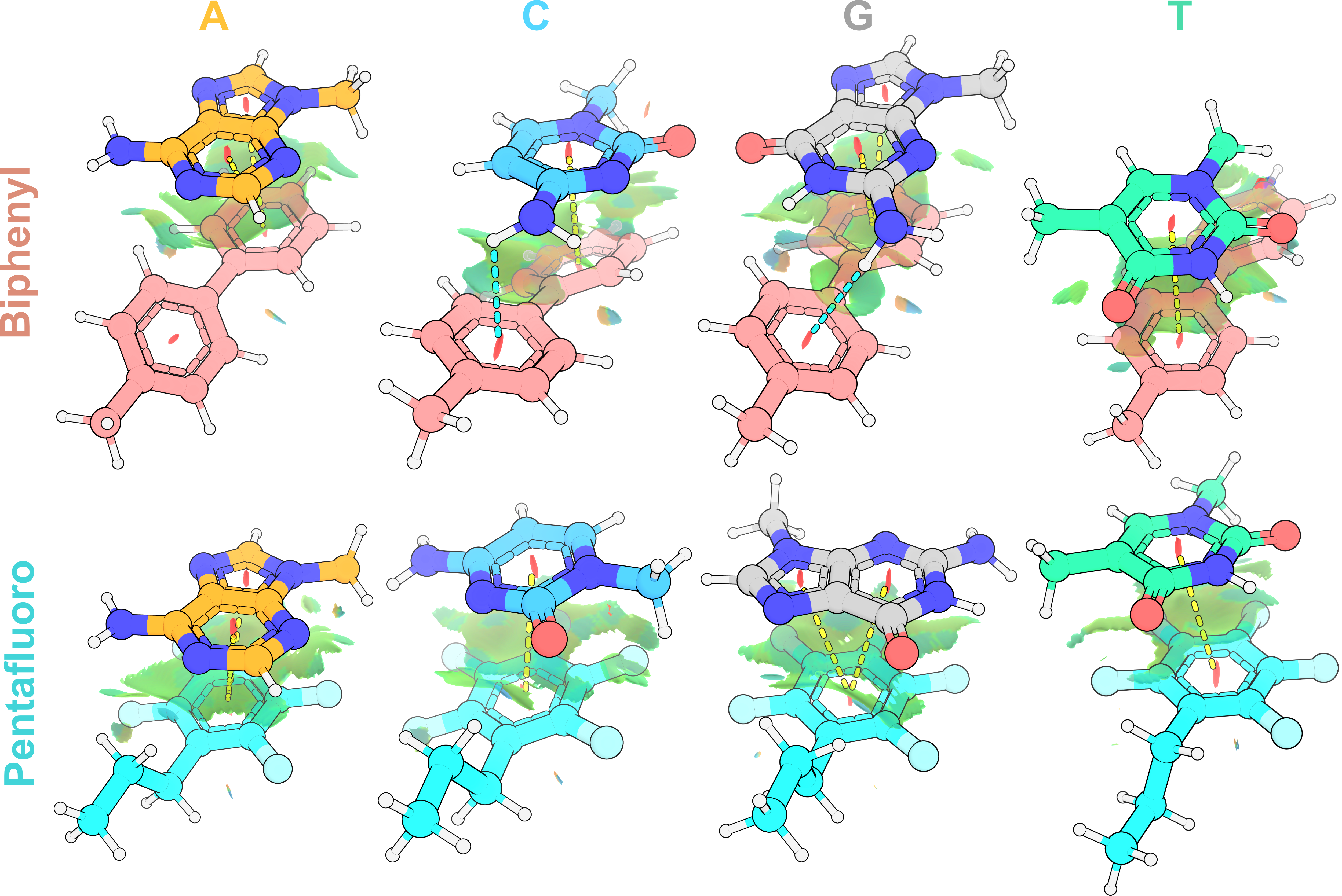
In fine, ces calculs de dynamique moléculaire ont nécessité la mise en place de calculs de mécanique quantique (QM), notamment pour dériver des paramètres modifiés de champs de force adaptés aux petites molécules et autres résidus non standards. D’autres utilisations de calculs QM incluent l’exploration de conformations de petites molécules (illustrer dans la Section 5.3.1.1), et l’étude d’interactions non-covalentes entre des nucléobases et des dérivés phényles servant de ligands de phase stationnaire chromatographique (Section 5.6.5).

Je me suis donc attaché à mettre en place des processus de calcul (Section 5.6.2) et de traitements de données (Section 5.6.2.2) aussi rapides et automatisés que possible, et pouvant tenir compte de contraintes RMN ou non. Le titre de ce manuscrit mentionne des structures non canoniques ; on abordera en fait deux aspects distincts :

• Les structures secondaires bizarres, sans se limiter aux G4s. J’illustrerai cela avec l’exemple de la résolution de la structure d’un complexe aptamère d’ADN RKEC1·dopamine (Section 5.6.3)

• Les modifications de structures primaires, à l’image de ce que j’avais fait lors de mon séjour postdoctoral à l’Université de Colombie Britannique (Chapitre 2). C’est pour cette application que j’ai ajouté des calculs de QM en amont du flux MD. J’ai ainsi travaillé sur des doubles hélices hybrides ADN/ARN, dans lesquelles une des dT est modifiée en 2’ par un hexose lié par une courte chaîne. Je ne présente pas ici ces résultats non publiés, mais ceux d’autres applications auxquelles j’ai étendu cette méthodologie (Sections 5.3.1.1, 5.6.5, 5.6.4).

J’ai également travaillé sur des structures de protéines, que j’élude ici.⁴

⁴ Papier soumis (et pas encore rejeté), à Science, avec Cameron Mackereth, en collaboration avec Yvan Huc, qui est le porteur de ce projet.

5.6.2 Implémentation GPU, automatisation et analyse de simulations MD

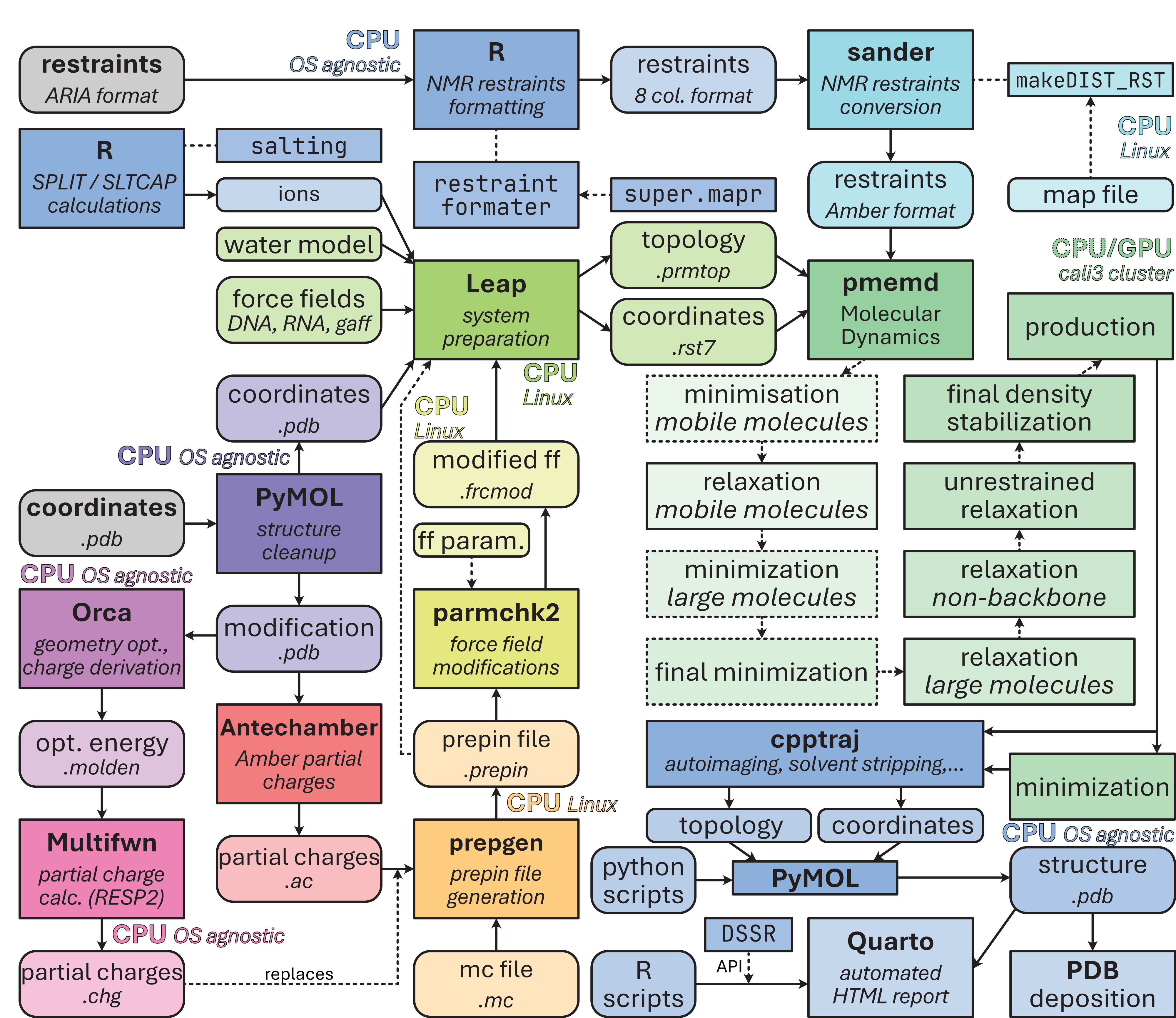
Les calculs de MD ont été effectués avec la suite logiciel Amber, en utilisant des champs de force… Amber. En réalité, le flux de travail que j’ai implémenté implique l’utilisation de plusieurs logiciels, certains inclus dans la suite Amber (Antechamber, Leap, pmemd, ccptraj) et d’autres non, notamment pour les calculs de QM en amont (Orca, Multifwn), la visualisation et modifications des structures (PyMOL), les scripts de calculs et visualisation des résultats (R, Python), et la génération de rapports d’analyse interactifs, robustes et reproductibles (Quarto) (Figure 5.36).

Figure 5.36. Flux de données pour les expériences de dynamique moléculaire avec Amber24, pouvant tenir compte de i. contraintes RMN et ii. modifications non-canoniques et ligands. Les coordonnées en entrées peuvent être le résultat de calculs consécutifs à des expériences RMN, ou tout autre source (pdb, structure “dessinées” manuellement). Après nettoyage de la structure dans PyMOL, les coordonnées peuvent êtres préparées dans Leap, où les champs de force ad hoc, le modèle de solvatation et les ions sont ajoutés. Le nombre de ces derniers doit permettre de neutraliser les charges des acides nucléiques. Pour ajuster la force ionique, les calculs de nombre de cations et anions à ajouter par les méthodes SPLIT/SLTCAP ont été implémentés dans R. Dans le cas de modification des acides nucléiques, ou de ligands non décrits dans les champs de force d’acides nucléiques (OL21, OL3), des modifications au champs de force doivent être importées dans Leap. Pour cela, la modification est isolée dans PyMOL, coiffée par des atomes permettant de correctement simuler son environnement chimique, si nécessaire, puis sa géométrie est optimisée par mécanique quantique, ici dans le logiciel ORCA. Après calcul de l’énergie de la structure optimisée et convertie en .molden, les charges partielles des atomes sont calculées par la méthode RESP2 implémentée dans le logiciel Multifwn. Un fichier de charges partielles compatible avec Amber est généré avec Antechamber, puis les charges y sont substituées par les charges RESP2. Enfin, prepgen et parmchk2 sont utilisés pour générés les fichiers permettant à Leap de lire les modifications et de les implémenter pour les atomes de la modification, sans importer les atomes de la coiffe, comme défini dans le fichier .mc. Les fichiers de topologies et coordonnées générés dans Leap sont soumis aux différentes étapes de dynamique moléculaire avec pmemd. Une préparation robuste du système en 10 étapes (ici présentée de façon simplifiée) a été implémentée à partir du protocole de Roe et Brooks [97]. Les étapes de relaxation et production MD utilise l’implémentation CUDA de pmemd que j’ai installé sur les serveurs de calculs DOREMI CALI v3 du Mésocentre de Calcul Intensif Aquitain de l’Université de Bordeaux. Les étapes de minimisation sont faites sur CPU à double précision pour éviter des overflow numériques si les forces mises en jeu sont élevées. Pour l’application de contraintes RMN, le fichier initial les décrivant est converti dans un format Amber via un script R, pour générer un fichier à 8 colonnes qui peut être lu et converti par le module pmemd au format Amber. Après production, une minimisation finale peut être effectuée si un ensemble doit être produit. Un pré-traitement des trajectoires est effectué en C++ avec cpptraj, puis les coordonnées finales sont converties en fichier pdb dans PyMOL. Les figures sont enfin générées avec des scripts Python et R dans un notebook Quarto permettant d’automatiser le traitement, la visualisation et la publication des données.

5.6.2.1 Implémentation sur GPU

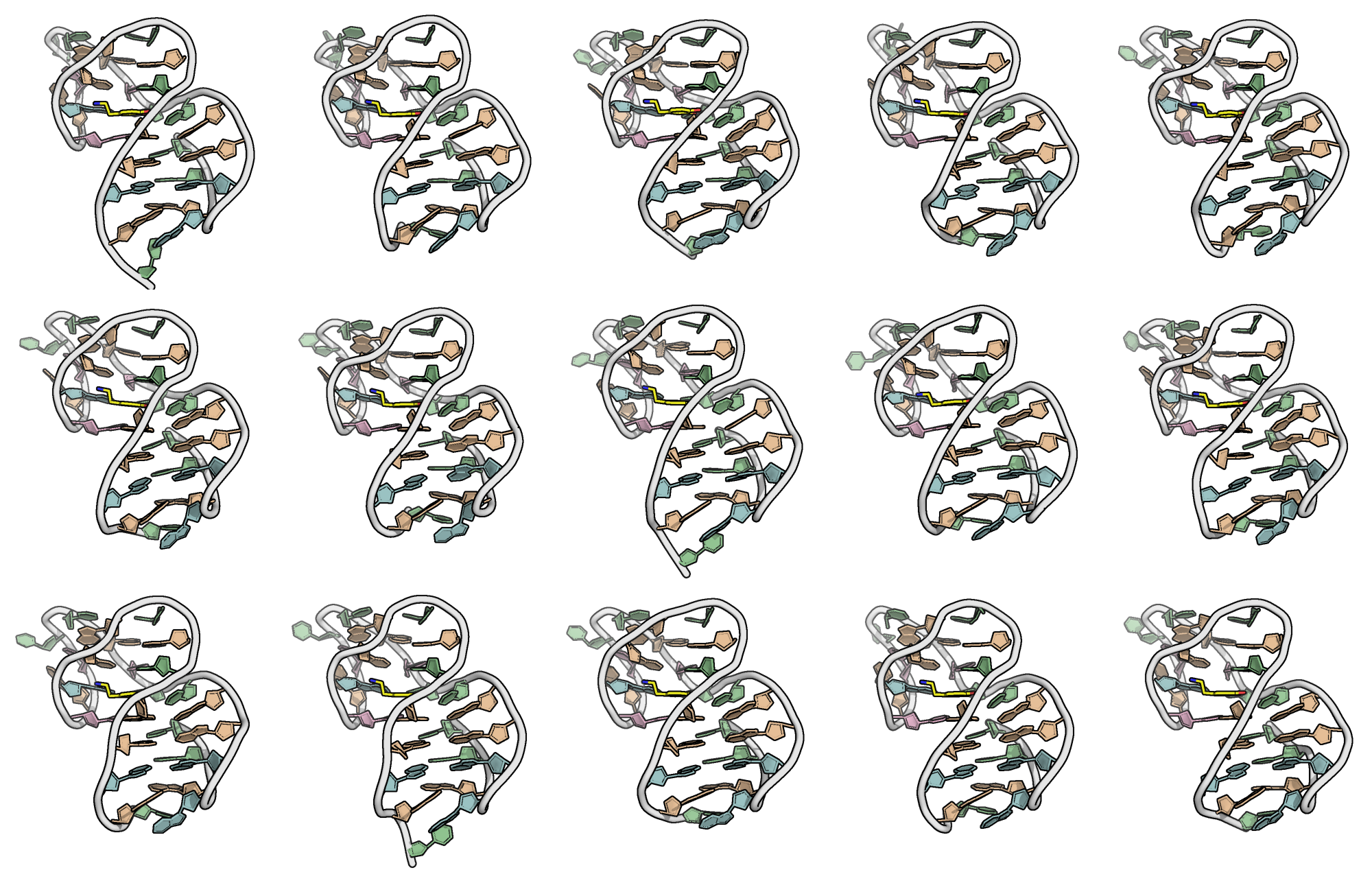
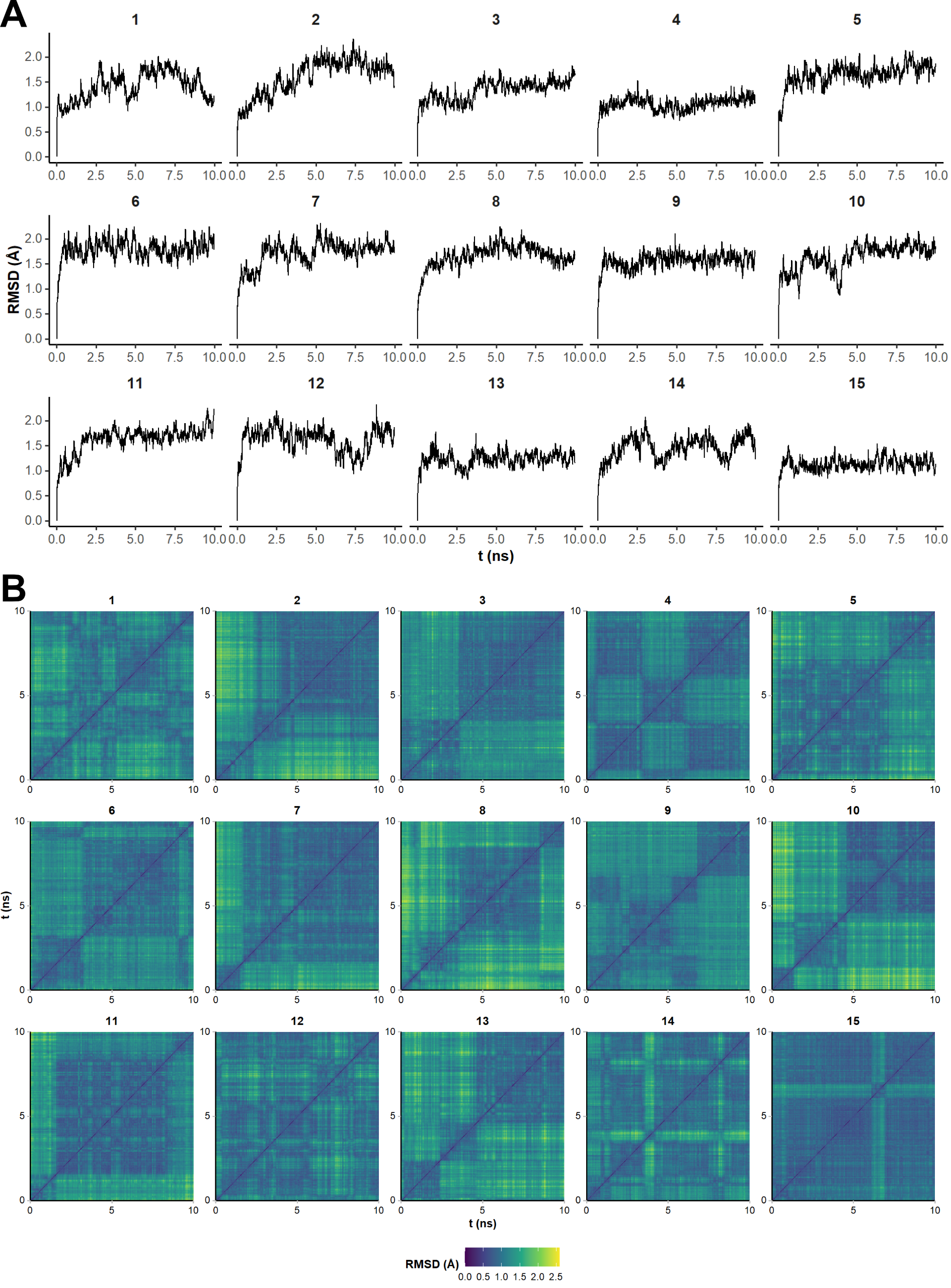
Les systèmes présentés ici sont composés d’une ou plusieurs chaînes ADN ou ARN (ou protéique) comprenant plusieurs dizaines de résidus. Ils doivent être simulés dans un solvant explicite et en présence de sels, impliquant la présence de plusieurs dizaines de milliers d’atomes (~ 40 000 pour le complexe RKEC1·dopamine). Pour des calculs de trajectoires courtes (de l’ordre de 10 ns), ce qui est suffisant pour un dépôt de structure sur la PDB, les calculs de rMD peuvent conceptuellement être effectués sur un CPU d’ordinateur de bureau. Par exemple, avec mon CPU 13th gen Intel Core i7-13700 2.10 GHz, le complexe RKEC1·dopamine est simulé avec des vitesses de l’ordre de la nanoseconde par jour de calcul. Plusieurs calculs peuvent être facilement lancés en parallèle en allouant un cœur CPU par structure, ce qui m’a permis de générer 15 structures en une dizaine de jours.

Le calcul sur un CPU au laboratoire est donc possible mais lent. Pour des trajectoires de l’ordre de la microseconde, plus conformes à l’état de l’art pour étudier des dynamiques [98, 99], l’utilisation de CPU grand public est irréaliste.⁵ Fort heureusement, Amber bénéficie d’une implémentation CUDA qui permet des calculs bien plus rapides sur processeur graphique (GPU). J’ai donc installé cette implémentation sur les serveurs de calculs DOREMI CALI v3 du Mésocentre de Calcul Intensif Aquitain de l’Université de Bordeaux. Cela me permet d’effectuer les étapes de dynamique moléculaire avec le module pmemd.cuda (v. 18.0.0) d’AMBER [98–100], sur un GPU NVIDIA H100 PCIe Tensor core GPU (version CUDA 12.4) qui, pour le système RKEC1·dopamine, simule environ 400 ns par jour (Figure 5.37). Pour les étapes de minimisation, peu coûteuses, je privilégie les calculs sur CPU, avec des codes en double précision. En effet, les GPUs reposent souvent sur un modèle à précision fixe située entre la simple et la double précision, et il est possible que des forces extrêmement élevées (par exemple celles résultant de clash atomiques, en particulier en début de calcul) provoquent des dépassements dans les calculs à virgule flottante [97]. Tous les calculs de QM sont également implémentés sur CPU.

98. Götz, A.W., Williamson, M.J., Xu, D., Poole, D., Le Grand, S. et Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. Journal of Chemical Theory and Computation, 2012, 8, 1542.

99. Salomon-Ferrer, R., Götz, A.W., Poole, D., Le Grand, S. et Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. Journal of Chemical Theory and Computation, 2013, 9, 3878.

⁵ Il faudrait 2 ans et 9 mois pour une seule simulation d’une microseconde sur mon CPU de bureau.

100. Le Grand, S., Götz, A.W. et Walker, R.C. SPFP: Speed without compromiseA mixed precision model for GPU accelerated molecular dynamics simulations. Computer Physics Communications, 2013, 184, 374.

Figure 5.37. Poster présenté aux Journées Calcul et Données 2024

5.6.2.2 Analyse semi-automatisée des structures et trajectoires

Les trajectoires de MD génèrent des fichiers volumineux contenant une grande quantité d’informations exploitables. En aval de mon flux de production standardisé, j’ai développé une approche semi-automatisée pour le traitement et l’analyse de ces données. Compte tenu de la taille importante des fichiers, le flux d’analyse repose premièrement sur des scripts que j’ai écris pour le programme cpptraj, écrit en C++ et beaucoup plus performant que les langages interprétés effectuant les calculs en mémoire, tels que R ou Python (Figure 5.36). Cette approche permet de générer des fichiers de trajectoire beaucoup moins lourds (par exemple sans solvant) et de calculer de nombreux paramètres diagnostiques (RMSD, respect des contraintes RMN) et analytiques (distances interatomiques, angles dièdres, etc.).  Dans un second temps, je poursuis les calculs et produis les figures avec une combinaison de scripts R et Python (en particulier pour automatiser la production de figures dans PyMOL). Finalement, la production de rapports d’analyse automatisée avec Quarto est également garante de la robustesse de l’approche, et permet également l’inclusion d’éléments dynamiques et interactifs. Par exemple, pour la visualisation des trajectoires et structures, j’utilise Mol^*, un ensemble d’outils logiciels open source, accessible via le web [101]. Un exemple de rapport pour le système RKEC1·dopamine décrit ci-après est disponible en ligne.⁶

101. Sehnal, D., Bittrich, S., Deshpande, M., Svobodová, R., Berka, K., Bazgier, V., Velankar, S., Burley, S.K., Koča, J. et Rose, A.S. Mol* Viewer: modern web app for 3D visualization and analysis of large biomolecular structures. Nucleic Acids Research, 2021, 49, W431.

⁶ https://ericlarg4.github.io/Dopamine

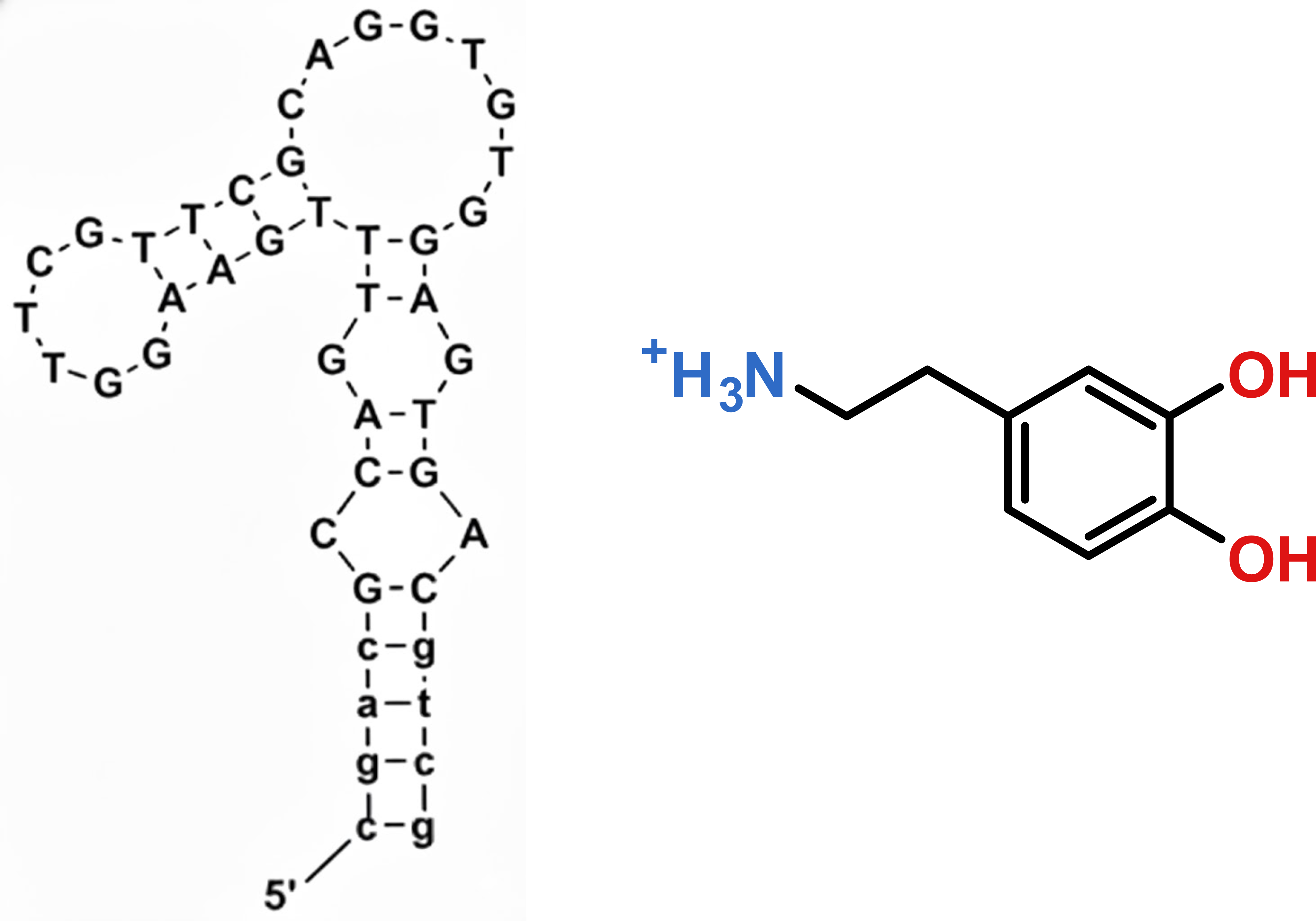
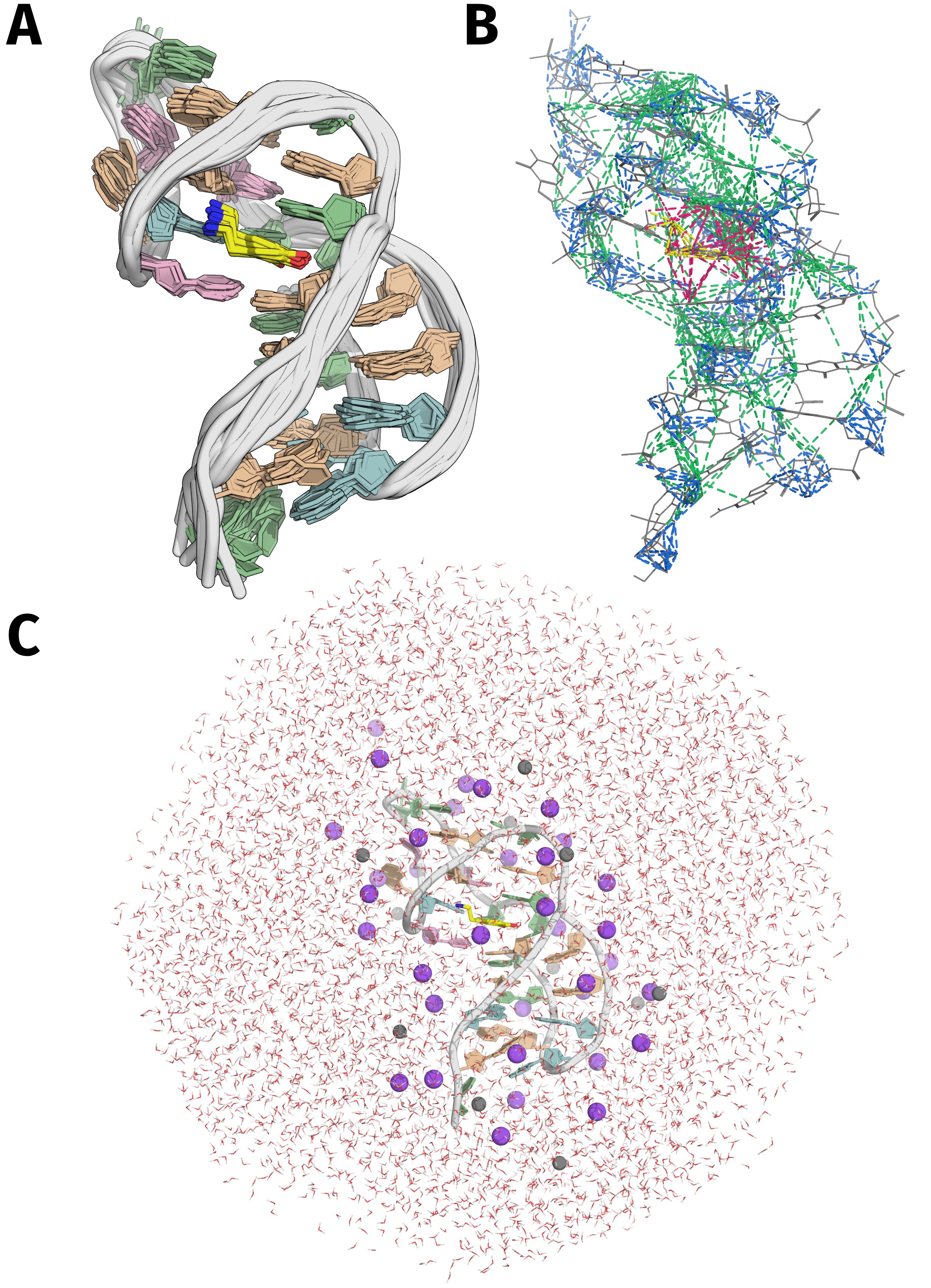
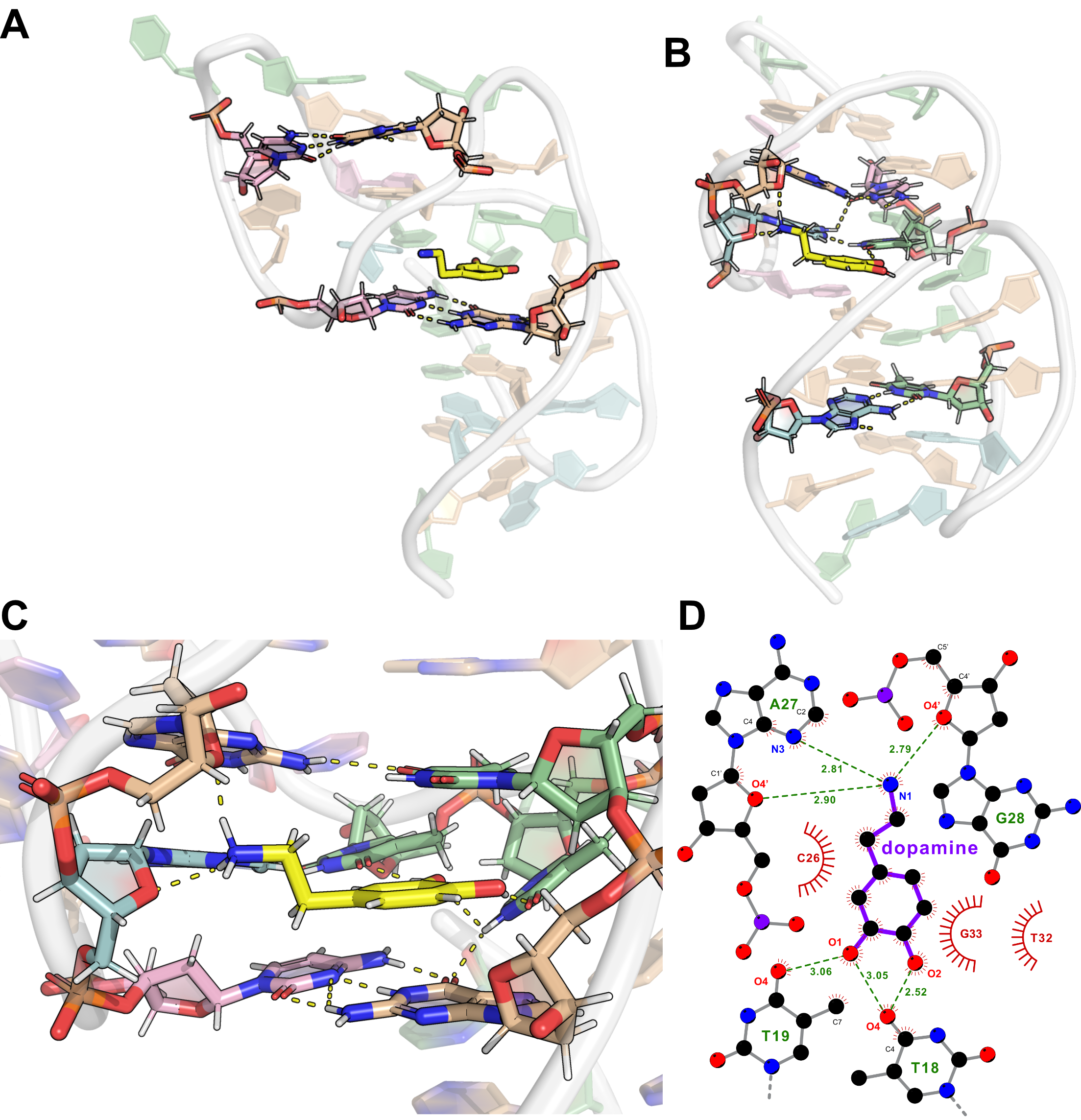
5.6.3 Exemple d’un complexe aptamère d’ADN RKEC1·dopamine

5.6.3.1 Contexte

L’équipe de Phillip Johnson (York University, Toronto, Canada) étudie des structures d’ARN et leurs complexes avec des protéines en combinant la RMN avec des techniques de biologie moléculaire et biophysique. Récemment, Phillip s’est intéressé aux structures d’aptamères, dont on connaît souvent peu. Les publications dans lesquelles sont décrites la sélection de ces séquences ne présentent généralement que des structures dans le plan, déterminées par mFold, et pas nécessairement correctes (Figure 5.38). Hors, les aptamères sont souvent utilisés comme biocapteurs, ce qui requiert de comprendre les mécanismes d’interactions avec leur cible. Dans ce contexte, Phillip collabore avec notre équipe pour caractériser des aptamères d’intérêt, comme RKEC1 qui se lie à la dopamine [102].

102. Kaiyum, Y.A., Hoi Pui Chao, E., Dhar, L., Shoara, A.A., Nguyen, M.-D., Mackereth, C.D., Dauphin-Ducharme, P. et Johnson, P.E. Ligand-Induced Folding in a Dopamine-Binding DNA Aptamer. ChemBioChem, 2024, 25.

Figure 5.38. Structure secondaire, incorrecte, publiée de l’aptamère de la dopamine (gauche, [103]) et dopamine (droite).

103. Nakatsuka, N., Yang, K.-A., Abendroth, J.M., Cheung, K.M., Xu, X., Yang, H., Zhao, C., Zhu, B., Rim, Y.S., Yang, Y., Weiss, P.S., Stojanović, M.N. et Andrews, A.M. Aptamerfield-effect transistors overcome Debye length limitations for small-molecule sensing. Science, 2018, 362, 319.

5.6.3.2 Préparation du système

Cameron Mackereth m’a fourni un set de 20 coordonnées du complexe RKEC1·dopamine, calculées dans ARIA par simulated annealing à partir de données RMN qu’il avait acquises (Figure 5.39A). De ces expériences, il a également déterminé des contraintes de distances. Le but pour moi était de mettre en place des calculs de rMD pour le dépôt de ces structures (nous en garderons 15) dans la PDB,⁷ mais aussi pour que ce flux de travail soit réutilisable dans le futur pour d’autres systèmes. Les grandes étapes ont été les suivantes :

⁷ https://www.rcsb.org/structure/unreleased/9HIO

1. Conversion des contraintes RMN du format ARIA vers un format à 8 colonnes, lisible par Amber, à l’aide d’un script R que j’ai développé. La fonction makeDIST_RST d’Amber a ensuite permis de générer le fichier de contrainte pour les simulations. De plus, un fichier de mapping a été préparé pour définir des noms communs pour les groupes de protons partageant une contrainte donnée (par exemple, les 3 atomes d’hydrogène du méthyl d’une thymine). Cette étape peut paraître triviale, mais sa semi-automatisation est garante de sa robustesse et un gain de temps significatif. Elle est également essentielle pour que la simulation ait lieu en tenant compte des données expérimentales. La figure Figure 5.39B illustre l’exhaustivité de ces contraintes.

2. Préparation du système à l’aide du programme leap de la suite Amber24 [104].

   1. Utilisation de champ de force OL21 pour l’ADN, OL3 pour l’ARN (non utilisé pour le complexe de dopamine), complété par le champs de force général d’Amber pour les molécules organiques (GAFF ; version 1.81), utile pour décrire les potentiels interatomiques des petites molécules [107]. Dans la plupart des cas, je ne me suis pas limité à GAFF et ai dérivé moi-même, par QM, les paramètres de champs de force des petites molécules et résidus modifiés.

   2. Solvation explicite dans une boîte octaédrique tronquée de molécules d’eau, en utilisant le modèle OPC avec les paramètres ad hoc Li/Merz des ions (ensemble 12-6) [109], avec un minimum de 14 Å entre le soluté et le bord de la boîte (Figure 5.39C). J’ai opté pour le modèle à 4 points OPC, plus coûteux que les modèles à 3 points classiquement utilisés comme TIP3P, car il reproduit de manière plus fidèle les propriétés thermodynamiques et structurales de l’eau liquide (densité, constante diélectrique), offrant ainsi une description plus réaliste des effets du solvant.

   3. Neutralisation des charges et ajustement de la force ionique : pour le complexe de dopamine, j’ai souhaité simuler une solution contenant 140 mM de NaCl, pour mieux refléter les conditions de SELEX dans lesquelles l’aptamère a été sélectionné. Pour cela, j’ai utilisé la méthode SLTCAP [110], dans laquelle les nombres d’ions requis (\(N_{\pm}\); ici 35 Na⁺ et 10 Cl^-) sont déterminés avec l’Équation 5.18, simplifiée par Machado and Pantano en l’Équation 5.19, où \(\nu_w\) est le volume d’eau de la boîte de simulation (environ \(3\times 10^5\) ų ici) en unités réduites, \(c_0\) la concentration en sel, \(Q\) la charge du système (ici, 25), et \(N_0 = \frac{N_w \times c_0}{55.5}\), avec \(N_w\) le nombre de molécules d’eau dans la boîte (ici, environ \(9\times10^4\)) [111]. Un point important ici est que la méthode SPLIT décrite par Machado et Pantano ne peut pas être appliquée car notre système ne satisfait pas à la condition \(N_0 \gg Q\) ; cependant, elle donne des valeurs identiques dans la plupart des cas ou ne diffère que d’un seul ion. \[N_{\pm}=\nu_w c_0 e^{\mp ArcSinh(\frac{Q}{2 \nu_w c_0})} \tag{5.18}\] \[N_{\pm}=N_0\sqrt{1+(\frac{Q}{2N_0})^2 \mp \frac{Q}{2}} \tag{5.19}\]

3. Préparation du système pour l’étape de production. Il est souvent nécessaire d’effectuer une série d’optimisations et/ou de simulations MD préparatoires afin de garantir la stabilité des simulations de production ultérieures, en particulier en présence d’un solvant explicite. Je me repose ici sur les travaux de Roe et Brooks, qui proposent un protocole simple, en dix étapes, applicable à une grande variété de systèmes [97]. Le protocole consiste en une série d’optimisations d’énergie et de relaxations progressives (4000 étapes de minimisation et 40 000 étapes de dynamique moléculaire, soit 45 ps au total). Le système est divisé en molécules mobiles, qui diffusent rapidement dans le système (eau, ions), et lourdes, plus lentes à diffuser. Les premières sont relaxées avant les secondes en appliquant des contraintes positionnelles sur ces dernières. De mêmes, les bases et chaînes latérales sont relaxées avant le squelette afin de permettre la relaxation de contacts atomiques sans perturbation des éléments de structure secondaire.

4. Production de 10 ns à 1 microseconde, en fonction des besoins, de MD à pression constante, en appliquant les contraintes RMN pondérées raisonnablement.

5. Minimisation finale (pour dépôt PDB) des points finaux de rMD, avec la même pondération des contraintes qu’en étape 4.

104. Case, D.A., Aktulga, H.M., Belfon, K., Cerutti, D.S., Cisneros, G.A., Cruzeiro, V.W.D., Forouzesh, N., Giese, T.J., Götz, A.W., Gohlke, H., Izadi, S., Kasavajhala, K., Kaymak, M.C., King, E., Kurtzman, T., Lee, T.-S., Li, P., Liu, J., Luchko, T., et al. AmberTools. Journal of Chemical Information and Modeling, 2023, 63, 6183.

107. Love, O., Galindo-Murillo, R., Zgarbová, M., Šponer, J., Jurečka, P. et Cheatham, T.E. Assessing the Current State of Amber Force Field Modifications for DNA─2023 Edition. Journal of Chemical Theory and Computation, 2023, 19, 4299.

109. Li, Z., Song, L.F., Li, P. et Merz, K.M. Systematic Parametrization of Divalent Metal Ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models. Journal of Chemical Theory and Computation, 2020, 16, 4429.

110. Schmit, J.D., Kariyawasam, N.L., Needham, V. et Smith, P.E. SLTCAP: A Simple Method for Calculating the Number of Ions Needed for MD Simulation. Journal of Chemical Theory and Computation, 2018, 14, 1823.

111. Machado, M.R. et Pantano, S. Split the Charge Difference in Two! A Rule of Thumb for Adding Proper Amounts of Ions in MD Simulations. Journal of Chemical Theory and Computation, 2020, 16, 1367.

97. Roe, D.R. et Brooks, B.R. A protocol for preparing explicitly solvated systems for stable molecular dynamics simulations. The Journal of Chemical Physics, 2020, 153.

Figure 5.39. Préparation du système RKEC1·dopamine. A. Ensemble de 20 structures obtenues par simulated annealing. B. Réseau de contraintes de distances intra (bleu) et inter-résidus (vert), intra-dopamine (jaune) et entre dopamine et RKEC1 (rose) converties au format Amber puis visualisées dans PyMOL avec un script Python. C. Solvation explicite du système, dont la force ionique est ajustée avec des ions sodium (violet) et chlorure (vert).

J’ai volontairement omis tous les paramètres expérimentaux des simulations. L’approche présentée ici est générale, robuste et reproductible, ce qui me permet désormais de traiter différents systèmes de manière cohérente et unifiée. 

Figure 5.40. Ensemble de 15 conformations du complexe RKEC1·dopamine déposé sur la PDB.

5.6.3.3 Analyse des résultats

Je présente ici quelques exemples d’exploitation typique des résultats, afin d’illustrer le flux de travail mis en place. Par exemple, il est courant d’analyser l’évolution temporelle de la RMSD pour évaluer la stabilité d’une simulation de dynamique moléculaire (Figure 5.41A). Ce type de représentation montre les fluctuations structurales de chaque conformère par rapport à la conformation initiale. Toutefois, ces figures peuvent prêter à confusion : deux conformères présentant une même valeur de RMSD ne sont pas nécessairement similaires. Ils sont simplement à une distance comparable du modèle de référence, mais peuvent différer considérablement l’un de l’autre. Pour pallier à ce biais de visualisation, je privilégie les représentations sous forme de matrices de similarité (des heatmaps dites pairwise RMSD ; Figure 5.41B), où chaque conformation est comparée à toutes les autres, offrant une vision plus complète de l’espace conformationnel échantillonné pendant la simulation. Ces figures permettent notamment de repérer facilement la formation de clusters structuraux au cours de la simulation, visibles par l’apparition de zones carrées le long de la diagonale.

Figure 5.41. A. RMSD unidimensionnelle sur tous les résidus (y compris les extrémités 5’ et 3’), sans hydrogène, pour l’ensemble des simulations contraintes (10 ns), la première structure étant utilisée comme référence. B. Pairwise RMSD (RMSD calculée pour toutes les paires de coordonnées) pour les quinze simulations. Cette représentation permet de mieux saisir l’étendue de la diversité structurelle au cours de la simulation, de repérer des clusters (carrés le long de la diagonale), et d’éviter le biais d’interprétation.

Dans le contexte de l’étude de structures non-canoniques, il est fréquent de mesurer des angles dièdres, notamment celui des liaisons glycosidiques \(\chi\) (correspondant au GBA dans la Section 5.4.1 ; Figure 5.42) et de torsion des sucres (pucker \(P\) ; Figure 5.43). J’ai développé des fonctions en R qui permettent de rapidement calculer chaque angle pour chaque nucléotide pour chaque set coordonnées extrait de la trajectoire (ici, 25000 ; Figures 5.42, 5.43). En particulier, \(P\) et son amplitude ont été calculés avec les équations 5.20 et 5.21, respectivement, en utilisant les angles de torsion \(\nu_i\) (atomes définis dans les équations 5.22–5.26).

\[ \tan P = \frac{(\nu_4 + \nu_1)-(\nu_3 + \nu_0)}{2\nu_2(\sin(\frac{\pi}{5}) + \sin(\frac{2\pi}{5}))} \tag{5.20}\]

\[ \theta_M = \frac{\nu_2}{\cos P} \tag{5.21}\]

\[\nu_0=C4'-O4'-C1'-C2' \tag{5.22}\] \[\nu_1=O4'-C1'-C2'-C3' \tag{5.23}\] \[\nu_2=C1'-C2'-C3'-C4' \tag{5.24}\] \[\nu_3=C2'-C3'-C4'-O4' \tag{5.25}\] \[\nu_4=C3'-C4'-O4'-C1' \tag{5.26}\]

Figure 5.42. Angle dièdre de la liaison glycosidique \(\chi\) de chaque nucléotide au cours de la simulation d’une microseconde (de l’intérieur vers l’extérieur), exprimé entre -180 et +180 degrés. On note ici que la guanine 31 est en conformation syn, alors que tous les autres nucléotides sont en anti, qui est la conformation attendue dans l’ADN duplex. Ces angles sont globalement stables pendant la simulation, ce que nous avons également observé en absence de contraintes de distance, preuve de la robustesse de la structure calculée.

Figure 5.43. Puckering \(P\) des sucres calculé avec la méthode d’Altona & Sundaralingam [112], représenté entre 0 et 360 degrés. Chaque point représente l’une des 25000 coordonnées extraites de la simulation d’une microseconde. La position des points par rapport au centre des cercles est fonction de l’amplitude \(\theta_M\) (plus l’amplitude est grande, plus le point est vers l’extérieur). La médiane est entourée en noir. L’ADN a normalement des puckers C2’-endo, et l’on peut considérer ici que tous les nucléotides colorés en marron, violet et rouge ont une configuration glycosidique canonique. Un exemple de pucker non canonique est T18, qui forme une liaison hydrogène avec la dopamine. Sa configuration en C1’-endo est très rare, mais a été observée autours d’intercalants et pour que la structure gagne en flexibilité [113, 114].

112. Altona, C. et Sundaralingam, M. Conformational analysis of the sugar ring in nucleosides and nucleotides. New description using the concept of pseudorotation. Journal of the American Chemical Society, 1972, 94, 8205.

113. Wang, A.H.J., Ughetto, G., Quigley, G.J. et Rich, A. Interactions between an anthracycline antibiotic and DNA: molecular structure of daunomycin complexed to d(CpGpTpApCpG) at 1.2-.ANG. resolution. Biochemistry, 1987, 26, 1152.

114. Shen, X., Gu, B., Che, S.A. et Zhang, F.S. Solvent effects on the conformation of DNA dodecamer segment: A simulation study. The Journal of Chemical Physics, 2011, 135.

Petite digression : la détermination d’angles dièdres, notamment \(\phi\) et \(\psi\), est également d’intérêt pour la validation de structures protéiques. Cette validation repose sur l’utilisation de serveurs web qui comparent les valeurs soumises à un set de référence d’angles “autorisés”, dont la provenance n’est pas toujours claire (Figure 5.44A). La mise en place d’analyse “maison” permet de sélectionner les données et leur analyse plus convenablement, ce que j’ai mis en place au laboratoire (Figure 5.44B).

Figure 5.44. Diagrammes de Ramachandran produits par PROCHECK (A) et par l’auteur avec un script en R (B), sur un ensemble de 20 complexes protéiques. Chaque point correspond à une valeur expérimentale. Les zones colorées représentent les zones autorisées, qui sont dérivées de données de références. Pour B, j’ai utilisé le jeu de données top2018 du laboratoire Richardson de l’Université Duke, déposé sur Zenodo [115]. Il contient des résidus de haute qualité issus de chaînes protéiques également de haute qualité, et de faible redondance dans la PDB [116].

115. Williams, C., Richardson, D. et Richardson, J. High quality protein residues: Top2018 mainchain-filtered residues. 2021, 10.5281/ZENODO.5777651.

116. Williams, C.J., Richardson, D.C. et Richardson, J.S. The importance of residue-level filtering and the Top2018 best-parts dataset of high-quality protein residues. Protein Science, 2021, 31, 290.

Un autre aspect très important de l’étude structurale est la mesure de distances interatomiques, notamment entre donneurs et accepteurs de liaisons hydrogène. Pour cela, j’ai développé un script permettant de visualiser la formation plus ou moins stable de liaisons hydrogènes sur des trajectoires entières, en fonction de critères géométriques plus ou moins strictes (angle et distance ; Figure 5.45). On note ici que trois liaisons hydrogène très stables sont formées au site d’interaction avec la dopamine, et que ces interactions sont conservées en absence de contraintes.

Figure 5.45. Formation de liaisons H au cours des simulations avec contraintes (rMD), sans contraintes (uMD) et en absence de dopamine (no LDP). La liste des liaisons H a été établie sur les structures minimisées des simulations rMD, avec une distance donneur-accepteur maximale de 3,1 Å, en conservant celles formées dans au moins 20 % des structures. Les liaisons H dans les régions 5’- et 3’ (résidus 11:17 et 33:37) sont colorées en bleu, et celles impliquant la dopamine en rose. En haut : chaque ligne est un point de temps (un point toutes les 0,04 ns) ; plus une ligne est foncée, plus la liaison H est courte et linéaire (la transparence suit linéairement le rapport angle/longueur de la liaison). En bas : Fréquences cumulées. La fréquence de formation des liaisons est indiquée pour des seuils moins strictes (3,5 Å et 120° ; couleurs claires) et plus stricts (3,0 Å et 140° ; couleurs foncées). Seules les liaisons H inter-résidus dont la fréquence « stricte » est supérieure à 0,10 sont représentées.

Un corollaire à ces considérations est la caractérisation de l’appariement de bases. Ici, nul n’est besoin de réinventer la roue. En fait, la roue a déjà été inventée plusieurs fois, et j’ai retenu trois classifications pour le traitement automatisé :

• Saenger a défini une liste de 28 paires de base (plus une, plus tard), identifiées par des chiffres romains [117, 118]. Une paire canonique Watson-Crick est XIX pour GC et XX pour AT.

• Leontis et Westhof [119], puis Lemieux et Major [120], on décrit les paires de base en fonction de i. l’établissement de liaisons H sur les faces Watson-Crick (W), Hoogsteen (H), ou sucre (S) et ii. l’orientation de la liaison glycosidique (syn/trans : c/t) des nucléotides. Une paire canonique est donc définie comme cWW.

• La classification DSSR, qui est similaire à la précédente, mais indique d’abord l’information c/t suivi par la faces interagissant définies comme Watson-Crick (W), grand sillon (major ; M, correspondant à H ci-dessus) et petit sillon (minor ; m, correspondant à S ci-dessus), entre lesquelles est intercalé + ou - pour indiquer si les brins sont parallèles ou antiparallèles [122]. Une paire canonique est alors définie comme cW-W.

117. Saenger, W. Principles of Nucleic Acid Structure Springer New York (1984).

118. Gesteland, R.F., Cech, T. et Atkins, J.F. The RNA World: The Nature of Modern RNA Suggests a Prebiotic RNA World Cold Spring Harbor Laboratory Press (2006).

119. LEONTIS, N.B. et WESTHOF, E. Geometric nomenclature and classification of RNA base pairs. RNA, 2001, 7, 499.

120. Lemieux, S. RNA canonical and non-canonical base pairing types: a recognition method and complete repertoire. Nucleic Acids Research, 2002, 30, 4250.

122. Lu, X.-J. DSSR-enabled innovative schematics of 3D nucleic acid structures with PyMOL. Nucleic Acids Research, 2020, 10.1093/nar/gkaa426.

Table 5.1. Résultats de la caractérisation automatisée des paires de base, ici pour une seule structure.

Ce que l’on peut humblement en retenir, c’est que (presque) tout a déjà été publié il y a au moins quarante ans, et qu’il suffit souvent de changer légèrement le vocabulaire pour redonner vie aux mêmes idées. Le lecteur attentif aura sans doute remarqué mon goût prononcé pour le recyclage de méthodes antérieures à ma propre naissance, comme en témoigne récemment mon intérêt pour l’HDX (mais il n’y avait pas de MS dans son implémentation initiale). Plus sérieusement, Lu et al. ont gentiment mis à disposition un serveur de calcul de ces classifications, ce qui m’a permis d’interroger automatiquement ledit serveur via l’API, en exploitant la librairie httr2 (Table 5.1) [123].

123. Wickham, H. httr2: Perform HTTP Requests and Process the Responses. 2023.

Ici, le complexe RKEC1·dopamine est remarquablement non canonique. Seules deux paires de bases respectent la géométrie Watson-Crick (Figure 5.46A). En plus des paires de bases non canoniques (Figure 5.46B), plusieurs triplets de bases, pas forcément coplanaires, sont formés, rendant la structure franchement bizarre.

Figure 5.46. A. Les deux seules paires de bases canoniques “WC” B. Exemples de paires de bases non canoniques “rWC”. C. Site d’interaction de la dopamine. D. Vue projetée dans le plan avec LigPlot⁺ [124]. Le ligand est en violet, les résidus en gris, les carbones, azotes et oxygènes en noir, bleu et rouge, respectivement, les liaisons hydrogènes en vert pointillés et les interactions hydrophobes sont symbolisées par des traits rouges.

124. Laskowski, R.A. et Swindells, M.B. LigPlot+: Multiple LigandProtein Interaction Diagrams for Drug Discovery. Journal of Chemical Information and Modeling, 2011, 51, 2778.

Finalement, la Figure 5.46C,D présente le site d’interaction de la dopamine, où celle-ci établit des liaisons hydrogène avec les T18 et T19 via les O1 et O2 de son cycle catéchol, tandis que l’ammonium interagit avec le N3 de l’adénine 27 et le sucre de G28. Cette interaction est nécessaire à la structuration de RKEC1, ce qui aura des implications sur la prédiction de cette structure. D’autres types d’analyse, notamment l’utilisation de la PCA, sont illustrés par ailleurs (Sections 5.3.1.1, 5.6.4).

5.6.3.4 Considérations sur la prédiction de structures

Ce manuscrit présente de nombreuses méthodes permettant de caractériser des structures d’acides nucléiques, leurs dynamiques et leurs interactions. Un sujet que je n’aborde pas, du fait de mon incompétence totale sur le sujet (pour le moment), est la prédiction de structures à partir d’une séquence, comme le permet AlphaFold par exemple. Avec l’expérience, on peut prédire si une séquence peut former un G4, et même proposer une topologie en suivant des règles simples,⁸ mais cela relève plus de la divination que de la science. Et quid de structures vraiment bizarres comme le complexe RKEC1·dopamine?

⁸ En solution potassium, les G4s à deux ou quatre tétrades sont antiparallèles, mais ceux à trois tétrades ne le sont jamais, les G4s à boucles court forment des G4s parallèles, etc.

125. Kretsch, R.C., Albrecht, R., Andersen, E.S., Chen, H.-A., Chiu, W., Das, R., Gezelle, J.G., Hartmann, M.D., Höbartner, C., Hu, Y., Jadhav, S., Johnson, P.E., Jones, C.P., Koirala, D., Kristoffersen, E.L., Largy, E., Lewicka, A., Mackereth, C.D., Marcia, M., et al. Functional relevance of CASP16 nucleic acid predictions as evaluated by structure providers. 2025.

Dans ce contexte, nous avons soumis au CASP16 (16th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction) la structure du complexe RKEC1·dopamine, que de nombreux groupes à travers le monde ont tenté de prédire à partir de la séquence. Des 107 modèles soumis, aucun ne s’est approché de la vérité (RMSD > 10 Å) [125]. Nous pouvons avancer deux explications. La première est le manque de diversité des structures d’ADN déposées dans la PDB. Le second problème est lié au fait que RKEC1 ne se structure qu’en présence de dopamine, mais il semble que de nombreux groupes aient calculé la structure en absence du ligand, avant de tenter d’intercaler celui-ci. Ces considérations montrent bien la nécessité du travail expérimental sur les aptamères que nous avons entrepris.

5.6.4 Application à des complexes G4/ligands.

Je présente brièvement ici une application récente du flux de travail MD développé dans l’équipe PRISM, une autre étant présentée dans la Section 5.3.1.1. Cette application s’inscrit dans un projet mené par Samir Amrane (ARNA ; Figure 5.47), qui développe des petites molécules possédant des propriétés antivirales (HIV-1, HCV or HPV) grâce à leur affinité pour les G4s. Dans l’étude qui nous intéresse ici, une nouvelle classe de ligands dibenzoacridinium (DBA) a été synthétisée et ses interactions avec des G4s caractérisées [126]. Les DBA ont une base acridine, comme BRACO19 (Figure 1.6), mais étendue et chargée positivement par quaternarisation de l’amine aromatique avec des dérivés phényliques. Des K_ds jusqu’à 0.1 µM et une activité anti-HIV-1 avec des IC₅₀ de l’ordre du micromolaire ont été mesurés pour les meilleurs complexes.

126. Kabbara, A., Buré, C., Guedin, A., Kauffmann, B., Largy, E., Marquevielle, J., Bonnafous, P., Mdarhri, Z., Ferrand, Y., Gabelica, V., Rosu, F., Andreola, M.-L., Olivier, C. et Amrane, S. Dibenzoacridinium derivatives as a new class of G-Quadruplex ligands with anti-HIV-1 properties. NAR Molecular Medicine, submitted.

Samir a montré par RMN que le dérivé DBA1 interagit avec la tétrade G2·G9·G12·G18 du G4 HIVpro1, en particulier avec G2, G9 et G18 (Figure 5.47A). Il lui fut alors suggéré par un pair de procéder à des expériences de docking pour déterminer plus précisément le mode d’interaction. S’il paraît très probable à ce stade que le ligand est stacké sur la tétrade, son orientation et la position de la charge positive sont inconnues.

Bien que le docking permette d’explorer rapidement divers modes d’interaction, la flexibilité intrinsèque des G4s rend ces derniers peu compatibles avec cette méthode. De plus, la structure résolue par RMN d’HIVpro1 montre que la tétrade G2·G9·G12·G18 est peu accessible pour un ligand. Il m’a donc paru nécessaire de mettre en place une approche hybride entre le docking, pour générer rapidement des modes d’interactions possibles, et la dynamique moléculaire pour tenir compte de la flexibilité du G4. Concrètement, après avoir dérivé les paramètres de champs de force de DBA1, j’ai procédé comme suit :

1. La tétrade G2·G9·G12·G18 a été rendue accessible en basculant les résidus stériquement encombrants vers l’extérieur, par MD basée sur OpenMM [127].

2. DBA1 a ensuite été docké sur la la tétrade avec LeDock [128], sans aucune contrainte de position, ce qui a généré un ensemble diversifié de modes d’interaction, non biaisés, que j’ai regroupé en sept clusters.

3. La meilleure pose (selon le score de docking) de chaque cluster a été soumise à une simulation MD de 50 ns, permettant aux résidus du site d’interaction de se replier vers la tétrade, lorsque cela était possible, et de former des interactions avec DBA1 qui n’auraient pas pu être capturées par le seul docking.

4. Les trajectoires obtenues ont été regroupées selon la géométrie du site d’interaction par PCA, donnant quatre modèles représentatifs reflétant les modes d’interactions les plus probables.

127. Helmich-Paris, B., Souza, B. de, Neese, F. et Izsák, R. An improved chain of spheres for exchange algorithm. The Journal of Chemical Physics, 2021, 155.

128. Wang, Z., Sun, H., Yao, X., Li, D., Xu, L., Li, Y., Tian, S. et Hou, T. Comprehensive evaluation of ten docking programs on a diverse set of proteinligand complexes: the prediction accuracy of sampling power and scoring power. Physical Chemistry Chemical Physics, 2016, 18, 12964.

Figure 5.47. A. Titration ¹H-RMN du G4 HIVpro1 avec DBA1 : superposition des spectres des protons imino (11.0–13.5 ppm) après addition progressive de DBA1 (0 à 2 équivalents molaires) au G4, à une concentration de 150 μM dans un tampon 20 mM de phosphate de potassium, 70 mM de KCl (90:10 H₂O/D₂O). B. Vue de dessus du site de d’interaction obtenue par combinaison de docking et de MD non restreinte, à partir de laquelle quatre structures représentatives ont été extraites. DBA1 est représenté en jaune, les guanines en brun, les cytosines en rose, les thymines en vert et les adénines en bleu. Encart : Samir Amrane.

Deux orientations distinctes de DBA1 ont été observées au sein des quatre clusters (Figure 5.47B). Dans tous les cas, DBA1 établit sans surprise des interactions \(\pi-\pi\) avec la tétrade, principalement G2 et G18. G12 reste largement non lié, conformément aux observations RMN. Dans les clusters 1 et 4, la structure en croissant de DBA1 se superpose avec la courbature de la tétrade, son groupe phényle s’insérant dans le sillon formé par les deux termini de HIVpro1. Ces clusters diffèrent par la position précise de DBA1, permettant un stacking supplémentaire avec la G19 en 3’ (cluster 1), ou avec la C10 d’une boucle (cluster 4). Dans cette même boucle, G11, qui est stacké la tétrade en l’absence de ligand, se stacke parfois au-dessus de DBA1.

En revanche, les clusters 2 et 3 présentent une orientation inversée de DBA1, avec l’azote de l’acridinium chargé positivement situé au-dessus du canal ionique. Cette configuration favorise le stacking avec T1 en 5’ et, dans le cluster 2, également avec C10. Dans le cluster 3, C10 se stacke sur G11 repositionné au-dessus de DBA1, formant ainsi une boucle latérale particulièrement structurée.

L’approche hybride docking/MD, couplée à des analyses PCA, a été particulièrement efficace pour l’étude de ce complexe ligand·G4. Bien qu’aucune contrainte n’ait été utilisée, ces simulations ont produit des résultats en parfait accord avec les expériences RMNs.

5.6.5 Étude des interactions \(\pi\)-\(\pi\) d’oligonucléotides avec des phases stationnaires aromatiques pour leur séparation en phase inverse sans agent d’appariement.

Je clos ce chapitre avec une étude à laquelle j’ai participé pendant l’été 2025 et qui, je trouve, résume assez bien ce manuscrit. Il y a tout dedans : de la chimie analytique et physique, de la chromatographie et de la spectroscopie, des interactions \(\pi-\pi\) (mes préférées), des oligonucléotides et des G4s auxquelles on ne s’attendait pas. Ça manque cruellement de spectrométrie de masse, mais on notera que l’approche chromatographique développée ici y est justement particulièrement adaptée.

Tout commence (pour moi) lorsque je participe à une journée organisée par le Club Sud-Ouest de l’Association Francophone des Sciences Séparative à Toulouse, lors de laquelle je présente certaines de mes activités de caractérisation d’oligonucléotides. J’y croise Davy Guillarme, de l’Université de Genève, qui me recontacte quelques jours plus tard pour me parler de séparation d’oligonucléotides par HPLC en phase inverse. Il connaît déjà mes modestes travaux de chromatographie chez Quality Assistance, puisqu’il a lui-même (beaucoup plus) travaillé sur ces thématiques.⁹

⁹ Notamment avec Valentina D’Atri, une ancienne postdoc de l’équipe de Valérie Gabelica, que j’avais croisée lorsque j’y étais moi-même postdoc.

1. Largy, E., König, A., Ghosh, A., Ghosh, D., Benabou, S., Rosu, F. et Gabelica, V. Mass Spectrometry of Nucleic Acid Noncovalent Complexes. Chemical Reviews, 2021, 122, 7720.

Généralement, la rétention d’oligonucléotides, qui sont des polyanions hydrophiles, sur des phases stationnaires apolaires de phase inverse nécessite l’utilisation d’agents d’appariement [1]. Ce sont typiquement des cations qui forme des paires d’ions (ion pairs, IP) avec les analytes, neutralisant la charge apparente et augmentant la rétention. Ces cations portent un groupe hydrophobe dont la modification permet de moduler la rétention. L’IP-RP-LC souffre cependant d’un certain manque de résolution de certaines impuretés, est plus difficile à développer que la RP-LC classique, nécessite des temps d’équilibration plus longs, et les agents d’appariement sont souvent la cause d’une suppression de l’ionisation qui détériore le signal MS. Des approches orthogonales existent, comme l’échange d’anion (AEX, non compatible avec la MS en couplage direct) ou la chromatographie hydrophile (HILIC), qui ne permet pas non plus toujours la résolution d’impuretés critiques.

Partant de ce constat, Davy a souhaité développer une méthode de RP-LC sans agent d’appariement, en utilisant des colonnes greffées avec des dérivés de phényle, notamment un biphényle et un pentafluorophényle. L’hypothèse est que ces ligands permettent la rétention d’oligonucléotides par interactions \(\pi-\pi\), ne dépendant pas de la présence d’IP. Dans leur étude, Davy et un doctorant, Thanos Tsalmpouris, ont inclut des oligonucléotides modèles dX₂₀ (X = A, C, G, T) pour mieux comprendre l’influence de la séquence oligonucléotidique sur l’ordre d’élution des analytes (G < C < A < T). Ils souhaitaient comprendre cet ordre, et confirmer que les interactions \(\pi-\pi\) entre colonne et analytes sont possibles, et modulables par la nature du ligand.

Pour répondre à ces questions, j’ai construit des séries de complexes entre les 4 nucléobases d’ADN et 2 ligands de colonne, un biphényle et un propyl-pentafluorophényle. Pour chaque combinaison nucléobase/ligand, j’ai préparé 4 géométries par rotation de 90° de l’angle de twist, tel que définit dans un duplex [129], pour un total de 32 complexes. J’ai ensuite optimisé la géométrie de ces complexes avec la fonctionnelle hybride B3LYP (jeu de bases def2-TZVP + def2/J) avec une correction non-locale de la dispersion (DFT-NL), ce qui est nécessaire pour correctement tenir compte des forces de dispersion de London dans ces systèmes dominés par des interactions attractives de van der Waals [130]. Les énergies de ce type de systèmes sont généralement surestimées à cause de la superposition des jeux de bases (Basis Set Superposition Error, BSSE), que j’ai corrigée en implémentant une correction BB-CP (Boys-Bernardi Counterpoise Correction) [131]. Aux aspects quantitatifs, j’ai ajouté une étude qualitative de la nature de l’interaction en calculant les potentiels électrostatiques (ESP) et les indicateurs de régions d’interaction (Interaction Region Indicator, IRI, Figure 5.48)

129. Jerbi, J., Fink, R.F., Peña-García, J., Arias-Olivares, D., Contreras-García, J. et Cerón-Carrasco, J.P. Quantum Effects Explain the Twist Angle in the Helical Structure of DNA. ChemPhysChem, 2024, 25.

130. Grimme, S., Antony, J., Schwabe, T. et Mück-Lichtenfeld, C. Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules. Org. Biomol. Chem., 2007, 5, 741.

131. Brauer, B., Kesharwani, M.K. et Martin, J.M.L. Some Observations on Counterpoise Corrections for Explicitly Correlated Calculations on Noncovalent Interactions. Journal of Chemical Theory and Computation, 2014, 10, 3791.

Ces expériences ont permis de montrer que :

• La stabilité des complexes provient principalement d’interactions \(\pi-\pi\), dominées par les forces de dispersion. Les bases G et C bénéficient d’une stabilisation électrostatique supplémentaire grâce à une liaison polaire NH-\(\pi\) entre leur amine exocyclique et l’anneau non stacké du biphényle.

• Tous les complexes présentent des énergies d’interaction comprises entre −8 et −12 kcal/mol, en accord avec les énergies de stacking des bases nucléiques dans les hélices d’ADN [132]. L’interaction de plusieurs bases le long des oligonucléotides devrait donc fournir une stabilisation suffisante pour assurer leur rétention.

132. Mignon, P. Influence of the  -  interaction on the hydrogen bonding capacity of stacked DNA/RNA bases. Nucleic Acids Research, 2005, 33, 1779.

Figure 5.48. Géométries optimisées (niveau B3LYP + DFT-NL(VV10) / def2-TZVP) des complexes entre les bases d’ADN méthylées (de gauche à droite, A : orange, C : bleu, G : gris, T : vert) et les ligands de colonne biphényle (en haut, rouge) et propyl-pentafluoro (en bas, bleu clair). La surface IRI (niveau = 0,75) met en évidence les interactions de van der Waals (vert) et la répulsion stérique (rouge). Les interactions \(\pi-\pi\) canonique et la liaison polaire NH-\(\pi\) sont également indiquées par des pointillés jaunes et cyans, respectivement.

Cela ne suffit pas, cependant, à expliquer l’ordre rétention des oligonucléotides modèles en fonction de leur structure primaire. L’exemple le plus criant est dG₂₀, puisqu’il est très peu retenu alors que les guanines forment les complexes les plus stables. Bien sûr, les effets hydrophobes (C < G < A < T) contribuent très probablement [133]. Mais le lecteur attentif aura compris que le problème majeur réside dans le choix des séquences, que j’ai décidé d’illustrer par CD, car il s’agit bien ici d’une question de structure secondaire.

133. Fornstedt, T. et Enmark, M. Separation of therapeutic oligonucleotides using ion-pair reversed-phase chromatography based on fundamental separation science. Journal of Chromatography Open, 2023, 3, 100079.

Dans les conditions de chromatographie de cette étude (< 40% en méthanol ou acétonitrile, 50 mM d’acétate d’ammonium, pH 8.0), dT₂₀ et dC₂₀ sont très peu structurés, le second présentant un peu plus de stacking intramoléculaire transitoire (Figure 5.49). En revanche, dA₂₀, en simple hélice, et surtout dG₂₀, en G4, forment des structures secondaires. Leurs nucléobases impliquées dans ces conformations ne sont alors pas disponibles pour interagir avec la phase stationnaire, ce qui diminue leur rétention d’autant que la conformation est stable. Il n’est donc pas surprenant de voir dG₂₀ très peu retenu et, à l’inverse, le très hydrophobe et linéaire dT₂₀ le plus retenu.

Figure 5.49. A. Spectres CD de dA₂₀, dC₂₀, dG₂₀ et dT₂₀ (8 µM) à 20 °C, dans 50 mM d’acétate d’ammonium, pH 8.0, 10 % MeOH, reflétant le début du gradient LC sur la colonne biphényle. Des résultats similaires ont été obtenus pour d’autres pourcentages de départ et de fin de gradient. B. Expériences correspondantes de dénaturation thermique. Les spectres acquis à 60 °C sont mis en évidence en pointillés rouges.

Je me limite ici à ma modeste contribution à cette étude par ailleurs exhaustive et très informative [134]. Ce que je souhaite souligner, c’est qu’au-delà de l’étude elle-même, l’implémentation des approches de calcul que j’ai utilisées permettra l’étude, à un niveau théorique élevé, de complexes non covalents d’intérêt pour l’équipe PRISM, ou pour ARNA de manière plus générale. Par ailleurs, cette collaboration¹⁰ m’a fait prendre pleinement conscience de la valeur ajoutée d’ARNA dans le paysage scientifique. Notre connaissance fine des acides nucléiques nous rend certains résultats évidents, alors qu’ils ne le sont pas pour d’autres équipes, par ailleurs excellentes dans leur domaine d’expertise.

134. Tsalmpouris, A., Largy, E. et Guillarme, D. Systematic evaluation of phenyl stationary phases for oligonucleotide analysis without ion-pairing reagents. Journal of Chromatography A, 2025, 1762, 466395.

¹⁰ et d’autres que j’ai omises ici par soucis de concision.